题目内容
已知正方体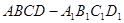 中,面
中,面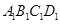 中心为
中心为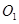 .
.
(1)求证: 面
面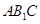 ;
;
(2)求异面直线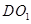 与
与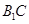 所成角.
所成角.
(1)对于线面平行的证明一般要利用其判定定理来求证。
(2)
解析试题分析:(1)证明:连结 ,设
,设 ,连结
,连结 ,则四边形
,则四边形 为平行四边形,
为平行四边形,
∴ 
又∵  ,
,
∴  面
面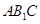 . 6分
. 6分
(2)解:由(1)可知, 为异面直线
为异面直线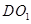 与
与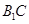 所成角(或其补角),
所成角(或其补角),
设正方体的边长2,则在 中,
中, ,
, ,
, ,
,
∴  为直角三角形,∴
为直角三角形,∴  . 6分
. 6分
考点:异面直线的角,线面平行
点评:解决的关键是熟练的根据几何中的性质定理和判定定理来求解,属于基础题。

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
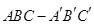 ,
,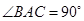 ,
,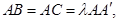 点M,N分别为
点M,N分别为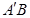 和
和 的中点.
的中点.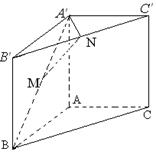
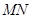 ∥平面
∥平面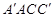 ;
;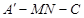 A为直二面角,求
A为直二面角,求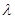 的值.
的值. 中,底面
中,底面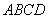 是边长为2的正方形,侧棱
是边长为2的正方形,侧棱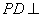 平面
平面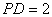 ,
,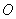 为底面对角线的交点,
为底面对角线的交点,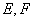 分别为棱
分别为棱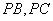 的中点
的中点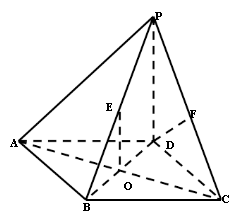
 //平面
//平面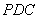 ;
;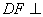 平面
平面 ;
;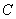 到平面
到平面 的距离。
的距离。 中,
中, ,
,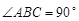 ,
,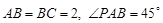 ,点
,点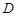 、
、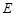 、
、 分别为
分别为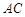 、
、 、
、 的中点.
的中点.
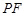 与平面
与平面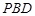 所成角的正弦值;
所成角的正弦值;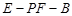 的大小.
的大小. 中,侧面
中,侧面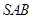 与侧面
与侧面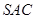 均为等边三角形,
均为等边三角形, 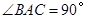 ,
,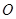 为
为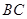 中点.
中点.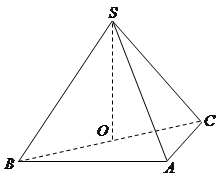
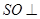 平面
平面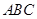 ;
; ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.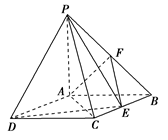
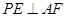 ;
;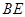 为何值时,
为何值时,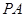 与平面
与平面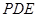 所成角的大小为45°.
所成角的大小为45°.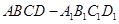 中,下底
中,下底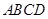 是边长为
是边长为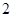 的正方形,上底
的正方形,上底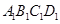 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱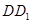 ⊥平面
⊥平面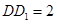 .
.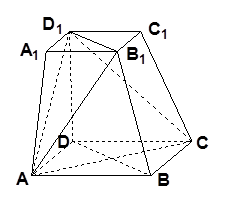
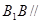 平面
平面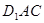 ;
;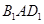 与平面
与平面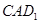 夹角的余弦值.
夹角的余弦值. 与等腰直角三角形
与等腰直角三角形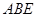 所在的平面互相垂直.
所在的平面互相垂直. ∥
∥ ,
, ,
,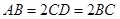 ,
, .
.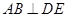 ;
;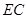 与平面
与平面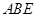 所成角的正弦值;
所成角的正弦值; 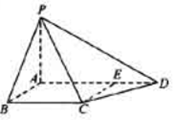
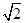 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积