题目内容
15.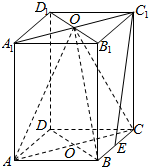 如图,ABCD-A1B1C1D1是长方体,已知AA1=AC=2,AB=$\sqrt{2}$,O、O1分别是上下底面ABCD和A1B1C1D1的对角线的交点,E是BC的中点.
如图,ABCD-A1B1C1D1是长方体,已知AA1=AC=2,AB=$\sqrt{2}$,O、O1分别是上下底面ABCD和A1B1C1D1的对角线的交点,E是BC的中点.(1)求证:C1E∥平面ABO1;
(2)求证:BD⊥平面ACO1;
(3)求点A到平面BCO1的距离.
分析 (1)设AB的中点为F,连结EF、FO1,推导出四边形EFO1C1是平行四边形,由此能证明C1E∥平面ABO1.
(2)推导出四边形ABCD是正方形,从而BD⊥AC,由此能证明BD⊥平面ACO1.
(3)由${V}_{A-BC{D}_{1}}={V}_{{O}_{1}-ABC}$,利用等体积法能求出点A到平面BCO1的距离.
解答  (本小题满分14分)
(本小题满分14分)
证明:(1)如图,设AB的中点为F,连结EF、FO1.
∵O、O1分别是上下底面ABCD和A1B1C1D1的对角线的交点,E是BC的中点,
∴EF∥AC,且EF=$\frac{1}{2}AC$.…(1分)
而C1O1=$\frac{1}{2}{A}_{1}{C}_{1}$,
又∵AC∥A1C1,且AC=A1C1,
∴EF∥C1O1,且EF=C1O1,∴四边形EFO1C1是平行四边形,
∴C1E∥FO1.…(3分)
又∵FO1?平面ABO1,C1E?平面ABO1,∴C1E∥平面ABO1.…(4分)
(2)∵ABCD-A1B1C1D1是长方体,且AA1=AC=2,AB=$\sqrt{2}$,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{4-2}=\sqrt{2}$,∴四边形ABCD是正方形,∴BD⊥AC.…(6分)
连结OO1,∵O、O1分别是上下底面ABCD和A1B1C1D1的对角线的交点,
∴OO1⊥平面ABCD,从而有BD⊥OO1.…(7分)
∵AC、OO1?平面ACO1,且AC∩OO1=O,∴BD⊥平面ACO1.…(8分)
解:(3)∵CO1=$\sqrt{C{{C}_{1}}^{2}+{O}_{1}{{C}_{1}}^{2}}$=$\sqrt{5}$,BO1=$\sqrt{5}$,
∴△BCO1是等腰三角形,连结EO1,EO1⊥BC,
且EO1=$\sqrt{C{{O}_{1}}^{2}-(\frac{BC}{2})^{2}}$=$\sqrt{(\sqrt{5})^{2}-(\frac{\sqrt{2}}{2})^{2}}$=$\frac{3\sqrt{2}}{2}$.…(9分)
∴${S}_{△BC{D}_{1}}$=$\frac{1}{2}BC•E{O}_{1}$=$\frac{1}{2}×\sqrt{2}×\frac{3\sqrt{2}}{2}$=$\frac{3}{2}$.…(10分)
设点A到平面BCO1的距离为h,则三棱锥A-BCO1的体积${V}_{A-BC{D}_{1}}$•h=$\frac{1}{3}×\frac{3}{2}h$=$\frac{h}{2}$.…(11分)
又三棱锥O1-ABC的体积${V}_{{O}_{1}-ABC}$=$\frac{1}{3}{S}_{△ABC}•O{O}_{1}$=$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{2}×2$=$\frac{2}{3}$.…(12分)
∵${V}_{A-BC{D}_{1}}={V}_{{O}_{1}-ABC}$,即$\frac{h}{2}=\frac{2}{3}$,解得h=$\frac{4}{3}$,即点A到平面BCO1的距离为$\frac{4}{3}$.…(14分)
点评 本题考查线面平行、线面垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意等体积法的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{2015}{2016}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{4028}{2015}$ | D. | $\frac{2014}{4030}$ |
 四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠A=60°,PC⊥平面ABCD,PC=a,E为PA的中点,
四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠A=60°,PC⊥平面ABCD,PC=a,E为PA的中点,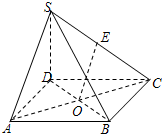 如图四棱锥S-ABCD中,SD⊥AD,SD⊥CD,E是SC的中点,O是底面正方形ABCD的中心,AB=SD=6.
如图四棱锥S-ABCD中,SD⊥AD,SD⊥CD,E是SC的中点,O是底面正方形ABCD的中心,AB=SD=6. 如图,AB为圆柱的轴,CD为底面直径,E为底面圆周上一点,AB=1,CD=2,CE=DE.
如图,AB为圆柱的轴,CD为底面直径,E为底面圆周上一点,AB=1,CD=2,CE=DE.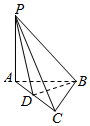 在三棱锥P-ABCD中,底面ABC为直角三角形,AB=BC,PA⊥平面ABC.
在三棱锥P-ABCD中,底面ABC为直角三角形,AB=BC,PA⊥平面ABC. 已知在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,左顶点为A(-3,0),圆心在原点的圆O与椭圆的内接三角形△AEF的三条边都相切.
已知在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,左顶点为A(-3,0),圆心在原点的圆O与椭圆的内接三角形△AEF的三条边都相切.