题目内容
2.求下列函数的单调区间:(1)y=3x-x3;
(2)f(x)=x3-$\frac{{x}^{2}}{2}$-2x+5;
(3)f(x)=2x2-lnx.
(4)y=2x2-5x+4.
分析 根据导数与函数单调性的关系求出单调区间.
解答 解:(1)y′(x)=3-3x2,令3-3x2=0得x=-1或x=1.
∴当x<-1或x>1时,y′<0,当-1<x<1时,y′>0.
∴y=3x-x3的增区间是[-1,1],减区间是(-∞,-1),(1,+∞).
(2)f′(x)=3x2-x-2,令3x2-x-2=0,解得x=-$\frac{2}{3}$或x=1.
∴当<-$\frac{2}{3}$或x>1时,f′(x)>0,当-$\frac{2}{3}$<x<1时,f′(x)<0.
∴f(x)=x3-$\frac{{x}^{2}}{2}$-2x+5的增区间是(-∞,-$\frac{2}{3}$),(1,+∞),减区间是(-$\frac{2}{3}$,1).
(3)f(x)的定义域为{x|x>0},f′(x)=4x-$\frac{1}{x}$,令4x-$\frac{1}{x}$=0,解得x=$\frac{1}{2}$或x=-$\frac{1}{2}$(舍).
∴当0<x$<\frac{1}{2}$时,f′(x)<0,当x$>\frac{1}{2}$时,f′(x)>0,
∴f(x)=2x2-lnx的增区间是($\frac{1}{2}$,+∞),减区间是(0,$\frac{1}{2}$).
(4)y=2x2-5x+4的图象开口向上,对称轴为x=$\frac{5}{4}$.
∴y=2x2-5x+4的增区间是($\frac{5}{4}$,+∞),减区间是(-∞,$\frac{5}{4}$).
点评 本题考查了导数与函数单调性的关系,属于基础题.

练习册系列答案
相关题目
13.已知实数x、y满足不等式组$\left\{\begin{array}{l}{2x-y≤6}\\{x-y-2≥0}\\{x≥a}\end{array}\right.$,若z=3x+y的最小值是8,则实数a=( )
| A. | 2 | B. | -$\frac{2}{7}$ | C. | 14 | D. | $\frac{14}{5}$ |
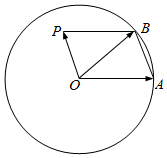 已知点A、B为单位圆O上的两点,点P为单位圆0所在平面内的一点,且$\overrightarrow{OA}$与$\overrightarrow{OB}$不共线.
已知点A、B为单位圆O上的两点,点P为单位圆0所在平面内的一点,且$\overrightarrow{OA}$与$\overrightarrow{OB}$不共线.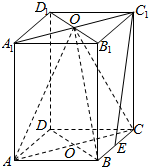 如图,ABCD-A1B1C1D1是长方体,已知AA1=AC=2,AB=$\sqrt{2}$,O、O1分别是上下底面ABCD和A1B1C1D1的对角线的交点,E是BC的中点.
如图,ABCD-A1B1C1D1是长方体,已知AA1=AC=2,AB=$\sqrt{2}$,O、O1分别是上下底面ABCD和A1B1C1D1的对角线的交点,E是BC的中点.