题目内容
4.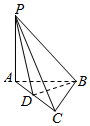 在三棱锥P-ABCD中,底面ABC为直角三角形,AB=BC,PA⊥平面ABC.
在三棱锥P-ABCD中,底面ABC为直角三角形,AB=BC,PA⊥平面ABC.(1)证明:BC⊥PB;
(2)若D为AC的中点,且PA=2AB=4,求点D到平面PBC的距离.
分析 (1)推导出BC⊥AB,BC⊥PA,由此能证明BC⊥PB.
(2)以A为原点,过A作BC的平行线为x轴,以AB为y轴,以AP为z轴,建立空间直角坐标系,利用向量法能求出点D到平面PBC的距离.
解答  证明:(1)∵底面ABC为直角三角形,AB=BC,
证明:(1)∵底面ABC为直角三角形,AB=BC,
∴BC⊥AB,
∵PA⊥平面ABC,BC?平面ABC,∴BC⊥PA,
∵AB∩PA=A,∴BC⊥PB.
解:(2)以A为原点,过A作BC的平行线为x轴,以AB为y轴,以AP为z轴,建立空间直角坐标系,
则P(0,0,4),B(0,2,0),C(2,2,0),D(1,1,0),
$\overrightarrow{BD}$=(1,-1,0),$\overrightarrow{BP}$=(0,-2,4),$\overrightarrow{BC}$=(2,0,0),
设平面PBC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BP}=-2y+4z=0}\\{\overrightarrow{n}•\overrightarrow{BC}=2x=0}\end{array}\right.$,取y=2,得$\overrightarrow{n}$=(0,2,1),
∴点D到平面PBC的距离d=$\frac{|\overrightarrow{n}•\overrightarrow{BD}|}{|\overrightarrow{n}|}$=$\frac{|-2|}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.
点评 本题考查异面直线垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案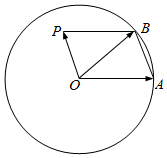 已知点A、B为单位圆O上的两点,点P为单位圆0所在平面内的一点,且$\overrightarrow{OA}$与$\overrightarrow{OB}$不共线.
已知点A、B为单位圆O上的两点,点P为单位圆0所在平面内的一点,且$\overrightarrow{OA}$与$\overrightarrow{OB}$不共线.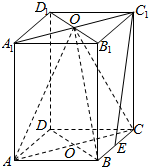 如图,ABCD-A1B1C1D1是长方体,已知AA1=AC=2,AB=$\sqrt{2}$,O、O1分别是上下底面ABCD和A1B1C1D1的对角线的交点,E是BC的中点.
如图,ABCD-A1B1C1D1是长方体,已知AA1=AC=2,AB=$\sqrt{2}$,O、O1分别是上下底面ABCD和A1B1C1D1的对角线的交点,E是BC的中点.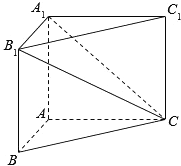 直三棱柱ABC-A1B1C1的底面是等腰直角三角形,AB=AC=2,四棱锥C-ABB1A1的体积等于4.
直三棱柱ABC-A1B1C1的底面是等腰直角三角形,AB=AC=2,四棱锥C-ABB1A1的体积等于4. 椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{2}}{2}$),且离心率为$\frac{\sqrt{2}}{2}$,过点P的动直线l与椭圆相交于A,B两点.
椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{2}}{2}$),且离心率为$\frac{\sqrt{2}}{2}$,过点P的动直线l与椭圆相交于A,B两点. 如图,一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{3}$.
如图,一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{3}$.