题目内容
已知等差数列{an}的前n项和为Sn,公差d≠0,且 成等比数列.
成等比数列.
(1)求数列{an}的通项公式;
(2)设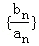 是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.
是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.
(Ⅰ) .(Ⅱ)
.(Ⅱ) .
.
解析试题分析:(Ⅰ)由已知 ,建立方程组
,建立方程组
求得 , 从而得到通项公式
, 从而得到通项公式 .
.
此类问题突出对等差数列、等比数列基础知识的考查,计算要细心.
(Ⅱ)不难得到 ,
, ,典型的应用“错位相消法”求和的一类问题.
,典型的应用“错位相消法”求和的一类问题.
在计算过程中,较易出错的是“相减”后,和式中的项数,应特别注意.
试题解析:(Ⅰ)依题意得
解得 ,
,
∴ ,
,
即 .
.
(Ⅱ) ,
,


两式相减得,
=
 .
.
考点:等差数列的通项公式、求和公式,等比数列,“错位相消法”.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 为等比数列,
为等比数列,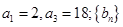 是等差数列,
是等差数列,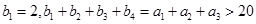
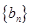 的通项公式及前
的通项公式及前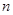 项和
项和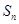 ;
;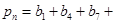
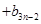 ,
,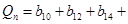
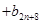 ,其中
,其中 ,试比较
,试比较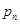 与
与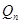 的大小,并加以证明.
的大小,并加以证明. 是公比大于1的等比数列,
是公比大于1的等比数列, 为数列
为数列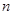 项和.已知
项和.已知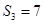 ,且
,且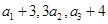 构成等差数列.
构成等差数列.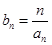 ,求数列
,求数列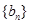 的前
的前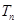 .
.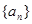 的前
的前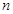 项的和为
项的和为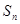 ,
, 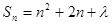 ,求证:数列
,求证:数列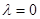 .
. ,公差
,公差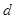 不为零,
不为零,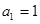 ,且
,且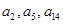 成等比数列;
成等比数列;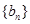 满足
满足 ,求数列
,求数列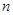 项和
项和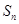 .
.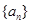 为递增数列,且
为递增数列,且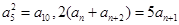 ,
,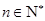 .
.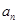 ;
;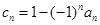 ,不等式
,不等式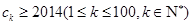 的解集为
的解集为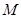 ,求所有
,求所有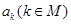 的和.
的和.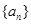 为等差数列,数列
为等差数列,数列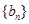 为等比数列,若
为等比数列,若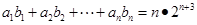 ,且
,且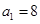 .
.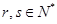 ,使得
,使得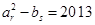 ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的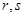 ;若不存在,请说明理由.
;若不存在,请说明理由.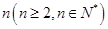 的两个数列
的两个数列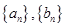 满足
满足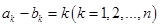 且集合
且集合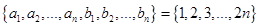 ,则称数列
,则称数列 项相关数列”.
项相关数列”.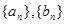 是一对“4项相关数列”,求
是一对“4项相关数列”,求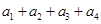 和
和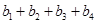 的值,并写出一对“
的值,并写出一对“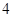 项相
项相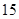 项相关数列”
项相关数列”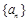 的前n项和为
的前n项和为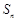 ,且
,且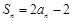 .
.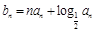 ,数列
,数列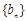 的前n项和为
的前n项和为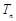 ,若不等式
,若不等式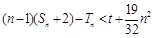 对任意
对任意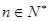 恒成立,求实数
恒成立,求实数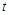 的取值范围.
的取值范围.