题目内容
已知 为等比数列,
为等比数列,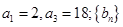 是等差数列,
是等差数列,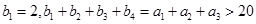
(Ⅰ)求数列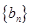 的通项公式及前
的通项公式及前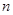 项和
项和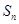 ;
;
(2)设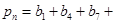
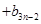 ,
,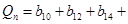
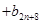 ,其中
,其中 ,试比较
,试比较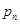 与
与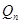 的大小,并加以证明.
的大小,并加以证明.
(Ⅰ)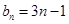 ,
,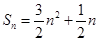 ;(Ⅱ)当
;(Ⅱ)当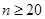 时,
时,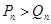 ;当
;当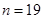 时,
时,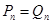 ;当
;当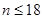 时,
时, .
.
解析试题分析:(Ⅰ)求数列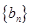 的通项公式及前
的通项公式及前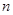 项和
项和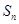 ,由已知
,由已知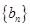 是等差数列,且
是等差数列,且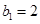 ,只需求出公差
,只需求出公差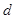 即可,由已知
即可,由已知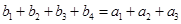 ,且
,且 为等比数列,
为等比数列,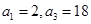 ,只需求出公比
,只需求出公比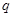 即可,由
即可,由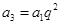 得,
得,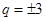 ,讨论是否符合条件
,讨论是否符合条件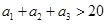 ,从而得
,从而得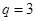 ,这样问就可以解决;(Ⅱ)设
,这样问就可以解决;(Ⅱ)设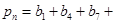
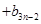 ,
,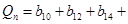
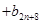 ,其中
,其中 ,试比较
,试比较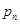 与
与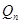 的大小,关键是求出
的大小,关键是求出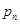 与
与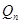 的关系式,由已知
的关系式,由已知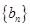 是等差数列,由(Ⅰ)知
是等差数列,由(Ⅰ)知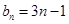 ,即可写出
,即可写出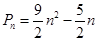 ,
, ,两式作差得
,两式作差得 ,讨论即可.
,讨论即可.
试题解析:(Ⅰ)设 的公比为
的公比为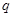 ,由
,由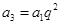 得,
得,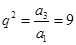 ,
,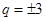 。 1分
。 1分
当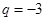 时,
时,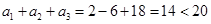 ,这与
,这与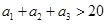 矛盾 2分
矛盾 2分
当 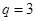 时,
时, ,符合题意。 3分
,符合题意。 3分
设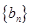 的公差为
的公差为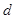 ,由
,由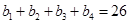 ,得:
,得: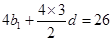
又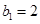
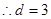
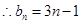 5分
5分
所以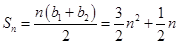 7分
7分
(Ⅱ)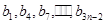 组成公差为
组成公差为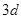 的等差数列,所以
的等差数列,所以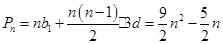 8分
8分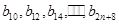 组成公差为
组成公差为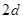 的等差数列, 所以
的等差数列, 所以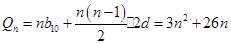
 10分
10分
故当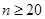 时,
时,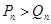 ;当
;当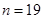 时,
时,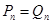 ;当
;当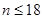 时,
时, 12分
12分
考点:等比数列,等差数列的通项公式,等差数列的前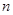 项和
项和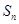 ,比较大小.
,比较大小.

练习册系列答案
相关题目
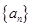 的前
的前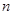 项和为
项和为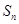 ,满足
,满足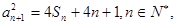 且
且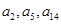 恰好是等比数列
恰好是等比数列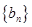 的前三项.
的前三项.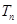 ,若对任意的
,若对任意的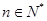 ,
,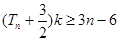 恒成立,求实数
恒成立,求实数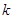 的取值范围.
的取值范围.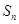 是数列
是数列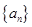 的前
的前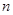 项和,对任意
项和,对任意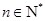 都有
都有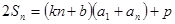 成立, (其中
成立, (其中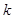 、
、 、
、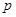 是常数).
是常数).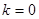 ,
,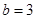 ,
,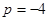 时,求
时,求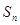 ;
;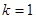 ,
,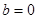 ,
,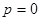 时,
时,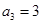 ,
,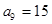 ,求数列
,求数列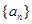 的通项公式;
的通项公式;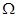 数列”.
数列”.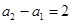 ,试问:是否存在数列
,试问:是否存在数列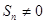 ,且
,且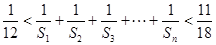 .若存在,求数列
.若存在,求数列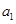 的所
的所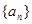 是等差数列,
是等差数列,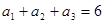 ,
,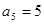 .
.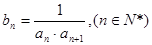 ,求数列
,求数列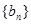 的前
的前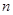 项和
项和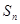 .
. 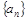 满足:
满足: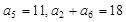 .
.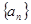 的通项公式;
的通项公式;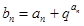 (
(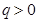 ),求数列
),求数列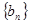 的前n项和
的前n项和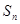 .
. 年,普通型汽车的总耗资费
年,普通型汽车的总耗资费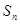 (万元)的表达式
(万元)的表达式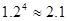
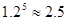
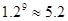
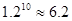 )
)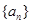 的前
的前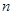 项和为
项和为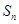 ,且
,且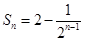 .
.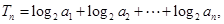 求证:
求证: .
.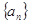 中,
中,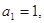 且点
且点 在直线
在直线 上。
上。 的通项公式;
的通项公式;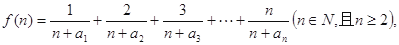 求函数
求函数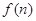 的最小值;
的最小值; 表示数列
表示数列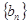 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于 的整式
的整式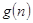 ,使得
,使得 对于一切不小于2的自然数
对于一切不小于2的自然数 成等比数列.
成等比数列.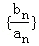 是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.
是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.