题目内容
已知等比数列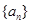 为递增数列,且
为递增数列,且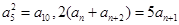 ,
,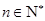 .
.
(Ⅰ)求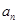 ;
;
(Ⅱ)令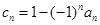 ,不等式
,不等式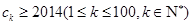 的解集为
的解集为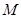 ,求所有
,求所有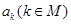 的和.
的和.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)要求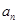 的通项公式,需要求出
的通项公式,需要求出 ,设
,设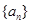 的首项为
的首项为 ,公比为
,公比为 ,根据
,根据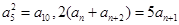 ,
,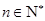 ,得
,得 ,
, ,解得
,解得 (舍)或
(舍)或 ,所以
,所以 .(Ⅱ)将
.(Ⅱ)将 代入
代入 得,
得, ,因为出现
,因为出现 ,需要分奇偶项讨论. 当
,需要分奇偶项讨论. 当 为偶数,
为偶数, ,即
,即 ,不成立,当
,不成立,当 为奇数,
为奇数, ,即
,即 ,而
,而 ,所以
,所以 ,则
,则 组成首项为
组成首项为 ,公比为
,公比为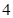 的等比数列,则所有
的等比数列,则所有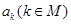 的和
的和 .
.
试题解析:(Ⅰ)设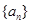 的首项为
的首项为 ,公比为
,公比为 ,
,
所以 ,解得
,解得
又因为 ,所以
,所以
则 ,
, ,解得
,解得 (舍)或
(舍)或
所以
(Ⅱ)则 ,
,
当 为偶数,
为偶数, ,即
,即 ,不成立
,不成立
当 为奇数,
为奇数, ,即
,即 ,
,
因为 ,所以
,所以
 组成首项为
组成首项为 ,公比为
,公比为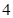 的等比数列
的等比数列
则所有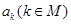 的和
的和 .
.
考点:1.等差、等比数列的性质;2.数列与不等式的简单应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 年,普通型汽车的总耗资费
年,普通型汽车的总耗资费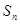 (万元)的表达式
(万元)的表达式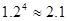
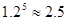
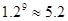
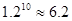 )
) ,
, ,
,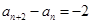
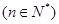
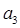

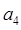 ,并求数列{an}通项公式;
,并求数列{an}通项公式; ,当
,当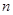 的值.
的值.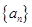 的公差
的公差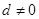 ,它的前
,它的前 项和为
项和为 ,若
,若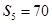 ,且
,且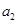 、
、 、
、 成等比数列.
成等比数列. 的前
的前 ,求证:
,求证: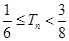 .
. 成等比数列.
成等比数列.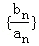 是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.
是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.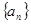 ,
,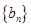 的通项
的通项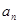 ,
,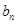 满足关系
满足关系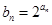 ,且数列
,且数列 项和
项和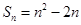
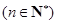 .
.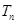 .
.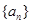 的首项
的首项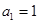 ,公差
,公差 .且
.且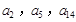 分别是等比数列
分别是等比数列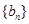 的
的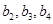 .
.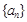 与
与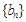 的通项公式;
的通项公式;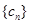 对任意自然数
对任意自然数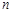 均有
均有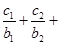
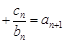 成立,求
成立,求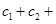
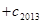 的值.
的值. 满足:
满足: ,
, .
. 及
及 的第n项为
的第n项为 ,若
,若 成等差数列,且
成等差数列,且 ,设数列
,设数列 的前
的前 项和
项和 .求数列
.求数列 、
、 满足
满足 .
. 时,求数列
时,求数列 ,
, ,求证:
,求证: .
.