题目内容
设 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 面积的最大值.
面积的最大值.
(1)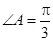 (2)
(2)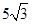
解析试题分析:(1)根据正弦定理将边的问题转化为角的问题,再利用两角和公式,也可利用余弦定理将角化为边的关系求解;(2)根据余弦定理求边的关系,再利用面积公式.
试题解析:(1)∵ ,所以
,所以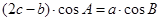 ,
,
∵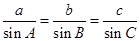 ,∴
,∴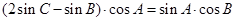 .
.
∴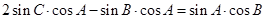 .∴
.∴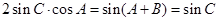 .
.
在△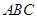 中,
中,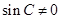 . ∴
. ∴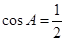 ,
,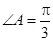 .
.
(2)∵ ,
, . ∴
. ∴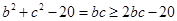
∴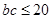 ,当且仅当
,当且仅当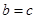 时取“="”" , ∴三角形的面积
时取“="”" , ∴三角形的面积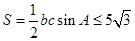 .
.
∴三角形面积的最大值为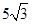 .
.
考点:正余项定理、两角和公式、三角形面积公式.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 ,设函数
,设函数 +1
+1 ,
,  ,求
,求 的值;
的值; ,且满足
,且满足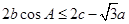 ,求
,求
 .
. ,求该三角形内切圆半径的取值范围。
,求该三角形内切圆半径的取值范围。 中,其中
中,其中 为定点,
为定点, 为动点,满足
为动点,满足 .
. 与
与 的关系式;
的关系式; 的面积分别为
的面积分别为 和
和 ,求
,求 的最大值,以及此时凸四边形
的最大值,以及此时凸四边形 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 ,
, .
. 的大小;
的大小;  ,求
,求 ,
, ,
, ,
, ,
, 请你用文字和公式写出计算A、C之间距离的步骤和结果.
请你用文字和公式写出计算A、C之间距离的步骤和结果.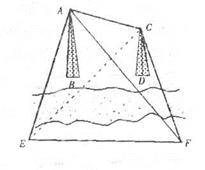
 中,
中, 分别是三个内角
分别是三个内角 的对边.若
的对边.若 ,
, ,
,  的值;
的值; .
. 中,已知
中,已知 ,D是BC边上一点,AD=10,AC=14,DC=6,求AB的长.
,D是BC边上一点,AD=10,AC=14,DC=6,求AB的长.
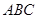 内的空地上植造“绿地
内的空地上植造“绿地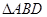 ”,其中
”,其中 ,
,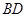 长可根据需要进行调节(
长可根据需要进行调节(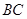 足够长),现规划在
足够长),现规划在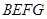 内种花,其余地方种草,设种草的面积
内种花,其余地方种草,设种草的面积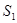 与种花的面积
与种花的面积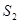 的比
的比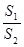 为
为 ,
,
 ,将
,将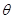 的函数关系;
的函数关系;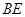 为多长时,
为多长时,