题目内容
14.已知a≥2,函数F(x)=min{x3-x,a(x+1)},其中min{p,q}=$\left\{\begin{array}{l}{p,p≤q}\\{q,p>q}\end{array}\right.$.(1)若a=2,求F(x)的单调递减区间;
(2)求函数F(x)在[-1,1]上的最大值.
分析 (1)令f(x)=x3-x,g(x)=a(x+1)=2(x+1),画出函数f(x),g(x)的图象,结合图象求出F(x)的递减区间即可;
(2)根据a的范围,在[-1,1]上,F(x)=f(x)=x3-x,求出F(x)的最大值即可.
解答 解:(1)令f(x)=x3-x,g(x)=a(x+1)=2(x+1),
令f(x)=g(x),解得:x=-1或x=2,
画出函数f(x),g(x)的图象,如图示: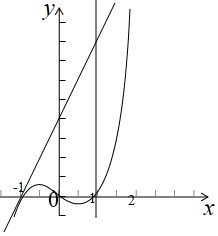 ,
,
显然x≤1时,f(x)≤g(x),x>1时,f(x)>g(x),
故F(x)=$\left\{\begin{array}{l}{{x}^{3}-x,x≤2}\\{2(x+1),x>2}\end{array}\right.$,
故F(x)在在(-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$)递减;
(2)由(1)得:a≥2时,F(x)=$\left\{\begin{array}{l}{{x}^{3}-x,x≤\frac{1+\sqrt{1+4a}}{2}}\\{a(x+1),x>\frac{1+\sqrt{1+4a}}{2}}\end{array}\right.$,
而$\frac{1+\sqrt{1+4a}}{2}$>2,
故在[-1,1]上,F(x)=f(x)=x3-x,
而f(x)在[-1,-$\frac{\sqrt{3}}{3}$)递增,在(-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$)递减,在($\frac{\sqrt{3}}{3}$,1]递增,
故F(x)的最大值是F(1)=0.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
4.“x-1>0”是“x2-1>0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.设x∈R,“x>1“的一个充分条件是( )
| A. | x>-1 | B. | x≥0 | C. | x≥1 | D. | x>2 |
9.函数y=sinx(cosx-sinx),x∈R的值域是( )
| A. | [-$\frac{1}{2}$,$\frac{3}{2}$] | B. | [$\frac{1-\sqrt{2}}{2},\frac{1+\sqrt{2}}{2}$] | C. | [-$\frac{3}{2},\frac{1}{2}$] | D. | [$\frac{-1-\sqrt{2}}{2},\frac{-1+\sqrt{2}}{2}$] |
6.函数f(x)=xm(1-x)n在区间[0,1]上的图象如图所示,则m,n的值为( )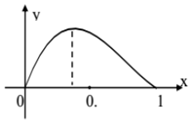

| A. | m=1,n=1 | B. | m=1,n=2 | C. | m=2,n=1 | D. | m=2,n=2 |
