题目内容

将一颗骰子掷两次，观察出现的点数，并记第一次出现的点数为m，第二次出现的点数为n，向量 $数学公式$ =（m，n）， $数学公式$ =（3，6），则向量 $数学公式$ 与 $数学公式$ 共线的概率为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

D
分析：利用古典概型的概率计算公式和向量共线定理即可得出．
解答：由题意可得：基本事件（m，n）（m，n=1，2，…，6）的个数=6×6=36．
若 $\text{[math]}$ ，则6m-3n=0，得到n=2m．满足此条件的共有（1，2），（2，4），（3，6）三个基本事件．
因此向量 $\text{[math]}$ 与 $\text{[math]}$ 共线的概率P= $\text{[math]}$ = $\text{[math]}$ ．
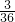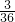故选D．
点评：熟练掌握古典概型的概率计算公式和向量共线定理是解题的关键．

练习册系列答案

探究与训练系列答案

点知教育中考试卷汇编及详解系列答案

南通小题课时作业本系列答案

名师面对面同步课堂系列答案

精英口算卡系列答案

小学生每日10分钟系列答案

天利38套高中名校期中期末联考测试卷系列答案

口算题应用题天天练神机妙算系列答案

应用题点拨系列答案

培优新方法系列答案

相关题目

已知f（3^x）= $数学公式$ ，则f（2）+f（4）+f（8）+…+f（2⁸）的值等于

A.
2007
B.
2008
C.
2015
D.
2016

三角形的两边边长分别为5和3，它们夹角的余弦是方程5x²-7x-6=0的根，则三角形的另一边长为

A.
52
B.
2 $数学公式$
C.
16
D.
4

四棱锥P-ABCD的三视图如图所示，四棱锥P-ABCD的五个顶点都在一个球面上，E、F分别是棱AB、CD的中点，直线EF被球面所截得的线段长为 $数学公式$ ，则该球表面积为________．

如图，用半径为2的半圆形铁皮卷成一个圆锥筒，那么这个圆锥筒的容积是________．

对于每个实数x，设f（x）取y=4x+1，y=x+2，y=-2x+4三个函数中的最小值，则f（x）的最大值为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

在数列{a_n}中， $数学公式$ ，若{a_n}是单调递增数列，则λ的取值范围为________．

已知椭圆 $数学公式$ 的离心率为 $数学公式$ ，短轴的一个端点到右焦点的距离为 $数学公式$ ，直线l：y=kx+m交椭圆于不同的两点A，B．
（1）求椭圆的方程；
（2）若坐标原点O到直线l的距离为 $数学公式$ ，求△AOB面积的最大值．

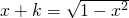关于x的方程 $数学公式$ 有两个相异实根，则k的范围是________．