题目内容
5．方程$\frac{x^2}{4-t}+\frac{y^2}{t-1}=1$表示曲线C，有下列命题①若曲线C为椭圆，则1＜t＜4，②若曲线C为双曲线，则t＜1或t＞4，③曲线C不可能是圆，④若曲线C表示椭圆且长轴在x轴，则$1＜t＜\frac{3}{2}$，则以上命题正确的有（ ）| A． | 2个 | B． | 3个 | C． | 1个 | D． | 4个 |
分析 根据曲线方程的特点，结合椭圆双曲线的标准方程分别判断即可．
解答 解：①当1＜t＜4且t≠$\frac{5}{2}$时，曲线表示椭圆，所以不正确；
②若曲线C表示双曲线，则（4-t）（t-1）＜0，解得t＞4或t＜1，所以正确；
③t≠$\frac{5}{2}$时，曲线C表示圆，不正确；
④若曲线C表示焦点在x轴上的椭圆，则4-t＞t-1＞0，解得1＜k＜$\frac{5}{2}$，所以不正确．
故选：C．
点评 本题主要考查圆锥曲线的方程，根据椭圆和双曲线的标准方程和定义是解决本题的关键．
练习册系列答案
相关题目
13．f（x）=$\left\{\begin{array}{l}{（3a-1）x+4a（x＜1）}\\{{a}^{x}（x≥1）}\end{array}\right.$是定义在（-∞，+∞）上是减函数，则a的取值范围是（ ）
| A． | [$\frac{1}{6}$，$\frac{1}{3}$） | B． | （0，$\frac{1}{3}$） | C． | （0，$\frac{1}{6}$] | D． | （$\frac{1}{3}$，1） |
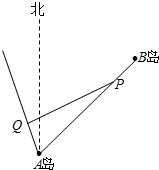已知海岛B在海岛A的北偏东45°的方向上，两岛相距10海里．小船P从海岛B以2海里/小时的速度沿直线向海岛A移动，同时小船Q从海岛A出发，沿北偏西15°方向以4海里/小时的速度移动．
20．命题“?x0∈R，3x0+$\frac{1}{{3}^{{x}_{0}}}$≤1”的否定为（ ）
| A． | ?x0∈R，3x0+$\frac{1}{{3}^{{x}_{0}}}$＞1 | B． | ?x0∈R，3x0+$\frac{1}{{3}^{{x}_{0}}}$≥1 | ||
| C． | ?x∈R，3x+$\frac{1}{{3}^{{x}$＞1 | D． | ?x∈R，3x+$\frac{1}{{3}^{{x}$＜1 |