题目内容
圆
,(θ为参数)的圆心到直线
,(t为参数)的距离是( )
|
|
| A、1 | ||
B、
| ||
C、
| ||
| D、3 |
考点:参数方程化成普通方程
专题:直线与圆,坐标系和参数方程
分析:先利用两式相加消去t将直线的参数方程化成普通方程,然后利用sin2θ+cos2θ=1将圆的参数方程化成圆的普通方程,求出圆心和半径,最后利用点到直线的距离公式求出圆心到直线的距离即可.
解答:
解:直线l的参数方程为
(参数t∈R),
∴直线的普通方程为3x+4y+10=0
圆C的参数方程为
(参数θ∈[0,2π]),
∴圆C的普通方程为(x-1)2+(y+2)2=9
∴圆C的圆心为(1,-2),d=
=1,
故选:A.
|
∴直线的普通方程为3x+4y+10=0
圆C的参数方程为
|
∴圆C的普通方程为(x-1)2+(y+2)2=9
∴圆C的圆心为(1,-2),d=
| |3-8+10| | ||
|
故选:A.
点评:本小题主要考查圆的参数方程及直线与圆的位置关系的判断,以及转化与化归的思想方法.本题出现最多的问题应该是计算上的问题,平时要强化基本功的练习,属于基础题.

练习册系列答案
相关题目
设i为虚数单位,则复数
为( )
| 3+4i |
| i3 |
| A、4+3i | B、4-3i |
| C、-4-3i | D、-4+3i |
已知集合A={0,1,2},B={x|ax+1=0},且A∪B=A,则实数a的取值集合是( )
A、{-1,-
| ||
| B、{-1,-2} | ||
| C、{0,-1,-2} | ||
D、{0,-1,-
|
若直线mx+ny+2=0(m>0,n>0)截得圆(x+3)2+(y+1)2=1的弦长为2,则
+
的最小值为( )
| 1 |
| m |
| 3 |
| n |
| A、6 | B、8 | C、10 | D、12 |
A={x|x>0},B={x|x>1},则A∩B=( )
| A、{x|0≤x<1} |
| B、{x|0<x≤1} |
| C、{x|x<0} |
| D、{x|x>1} |
对于函数f(x)=sin(πx+
),下列命题正确的是( )
| π |
| 2 |
| A、f(x)的周期为π,且在[0,1]上单调递增 |
| B、f(x)的周期为2,且在[0,1]上单调递减 |
| C、f(x)的周期为π,且在[-1,0]上单调递增 |
| D、f(x)的周期为2,且在[-1,0]上单调递减 |
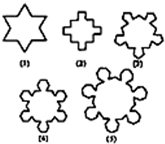 如图,第一个多边形是由正三角形“扩展”而来,第二个多边形是由正四边形“扩展”而来,…,如此类推,设由正n边形“扩展“而来的多边形的边数记为an.则
如图,第一个多边形是由正三角形“扩展”而来,第二个多边形是由正四边形“扩展”而来,…,如此类推,设由正n边形“扩展“而来的多边形的边数记为an.则