题目内容
函数y=x2(x>0)的图象在点(an,an2)处的切线与x轴交点的横坐标为an+1,n∈N*,若a1=16,则a3+a5=分析:首先对函数求导得到y′=2x,得到函数y=x2(x>0)的图象在点(an,an2)处的切线的斜率是2an,根据点斜式写出切线的方程,求出切线与横轴交点的横坐标,得到数列递推式,看出数列是一个等比数列,写出通项.
解答:解:∵对函数求导得到y′=2x
∴函数y=x2(x>0)的图象在点(an,an2)处的切线的斜率是2an
∴在点(an,an2)处的切线方程为:y-an2=2an(x-an),
∵切线与x轴交点的横坐标为an+1,
当y=0时,解得x=
an,
∴an+1=
an,
∴数列是一个公比为
的等比数列,
首项是16,
∴数列{an}的通项公式为16×(
)n-1=16×21-n=25-n
故答案为:25-n
∴函数y=x2(x>0)的图象在点(an,an2)处的切线的斜率是2an
∴在点(an,an2)处的切线方程为:y-an2=2an(x-an),
∵切线与x轴交点的横坐标为an+1,
当y=0时,解得x=
| 1 |
| 2 |
∴an+1=
| 1 |
| 2 |
∴数列是一个公比为
| 1 |
| 2 |
首项是16,
∴数列{an}的通项公式为16×(
| 1 |
| 2 |
故答案为:25-n
点评:本题考查数列和函数的综合,本题解题的关键是写出数列递推式,求出两个项之间的关系,得到数列是一个等比数列.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
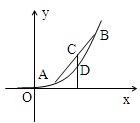 设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).
设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).