题目内容
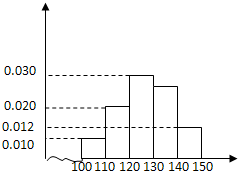 某校高三年级有400人,在省标准化考试中,用简单随机抽样的方法抽取容量为50的样本,得到数学成绩的频率分布直方图(如图).
某校高三年级有400人,在省标准化考试中,用简单随机抽样的方法抽取容量为50的样本,得到数学成绩的频率分布直方图(如图).(1)求第四个小矩形的高;
(2)估计该校高三年级在这次考试中数学成绩在120分以上的学生大约有多少人?
(3)样本中,已知成绩在[140,150]内的学生中有三名女生,现从成绩在[140,150]内的学生中选取3名学生进行学习经验推广交流,设有X名女生被选取,求X的分布列和数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图,离散型随机变量及其分布列
专题:概率与统计
分析:(1)由频率分布直方图的性质,能求出第四个小矩形的高.
(2)由频率分布直方图得数学成绩在120分以上的频率为0.7,由此可估计该校高三年级在这次考试中数学成绩在120分以上的学生人数.
(3)由频率分布直方图可知,样本中成绩在[140,150]内的学生共有6人,由题设知这6人恰好是3男3女,从而X的所有可能取值为0、1、2、3,分别求出相应的概率,由此能求出X的分布列和数学期望.
(2)由频率分布直方图得数学成绩在120分以上的频率为0.7,由此可估计该校高三年级在这次考试中数学成绩在120分以上的学生人数.
(3)由频率分布直方图可知,样本中成绩在[140,150]内的学生共有6人,由题设知这6人恰好是3男3女,从而X的所有可能取值为0、1、2、3,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答:
解:(1)由频率分布直方图可知,第四个小矩形的高为:
[1-(0.01+0.020+0.030+0.012)×10]÷10=0.028.(3分)
(2)∵样本中,数学成绩在120分以上的频率为:
1-(0.01+0.020)×10=0.7,(4分)
∴通过样本估计总体(即将频率看作概率),
可估计该校高三年级在这次考试中数学成绩
在120分以上的学生大约有400×0.7=280(人).(6分)
(3)由频率分布直方图可知,样本中成绩在[140,150]内的学生共有0.012×10×50=6(人).
于是,由题设知这6人恰好是3男3女.(7分)
∴X的所有可能取值为0、1、2、3,
P(X=0)=
=
,P(X=1)=
=
,
P(X=2)=
=
,P(X=3)=
=
.(10分)
∴X的分布列为:
∴X的数学期望为:EX=0×
+1×
+2×
+3×
=
.(12分)
[1-(0.01+0.020+0.030+0.012)×10]÷10=0.028.(3分)
(2)∵样本中,数学成绩在120分以上的频率为:
1-(0.01+0.020)×10=0.7,(4分)
∴通过样本估计总体(即将频率看作概率),
可估计该校高三年级在这次考试中数学成绩
在120分以上的学生大约有400×0.7=280(人).(6分)
(3)由频率分布直方图可知,样本中成绩在[140,150]内的学生共有0.012×10×50=6(人).
于是,由题设知这6人恰好是3男3女.(7分)
∴X的所有可能取值为0、1、2、3,
P(X=0)=
| ||
|
| 1 |
| 20 |
| ||||
|
| 9 |
| 20 |
P(X=2)=
| ||||
|
| 9 |
| 20 |
| ||
|
| 1 |
| 20 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 20 |
| 9 |
| 20 |
| 9 |
| 20 |
| 1 |
| 20 |
| 3 |
| 2 |
点评:本题考查频率分布直方图、随机变量的分布列、数学期望等概念及相关计算,考查运用概率知识与方法解决实际问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知全集U={x|0<x<9},A={x|1<x<a},若非空集合A⊆U,则实数a的取值范围是( )
| A、(-∞,9) |
| B、(-∞,9] |
| C、(1,9) |
| D、(1,9] |
一个几何体的三视图如图所示,则这个几何体的体积等于( )


| A、4 | B、6 | C、8 | D、12 |