题目内容
18.设函数f(x)=sin(ωx+φ),A>0,ω>0,若f(x)在区间[$\frac{π}{6}$,$\frac{π}{2}$]上单调,且f($\frac{π}{2}$)=f($\frac{2π}{3}$)=-f($\frac{π}{6}$),则f(x)的最小正周期为 ( )| A. | $\frac{π}{2}$ | B. | 2π | C. | 4π | D. | π |
分析 由题意求得x=$\frac{7π}{12}$,为f(x)=sin(ωx+φ)的一条对称轴,($\frac{π}{3}$,0)为f(x)=sin(ωx+φ)的一个对称中心,根据$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{3}$,解得ω的值.
解答 解:∵函数f(x)=sin(ωx+φ),A>0,ω>0,若f(x)在区间[$\frac{π}{6}$,$\frac{π}{2}$]上单调,
∴$\frac{π}{2}$-$\frac{π}{6}$≤$\frac{T}{2}$=$\frac{1}{2}•\frac{2π}{ω}$=$\frac{π}{ω}$,即$\frac{π}{3}$≤$\frac{π}{ω}$,∴0<ω≤3.
∵f($\frac{π}{2}$)=f($\frac{2π}{3}$)=-f($\frac{π}{6}$),
∴x=$\frac{\frac{π}{2}+\frac{2π}{3}}{2}$=$\frac{7π}{12}$,为f(x)=sin(ωx+φ)的一条对称轴,
且($\frac{\frac{π}{6}+\frac{π}{2}}{2}$,0)即($\frac{π}{3}$,0)为f(x)=sin(ωx+φ)的一个对称中心,
∴$\frac{T}{4}$=$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{3}$=$\frac{π}{4}$,解得ω=2∈(0,3],∴T=$\frac{2π}{2}$=π,
故选:D.
点评 本题考查三角函数的周期性及其求法,确定x=$\frac{7π}{12}$与($\frac{π}{3}$,0)为同一周期里面相邻的对称轴与对称中心是关键,也是难点,属于难题.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案| A. | 243 | B. | $27\root{5}{27}$ | C. | $\sqrt{3}$ | D. | 81 |
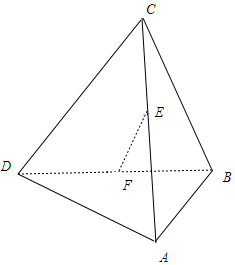
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | ?x∉R,x2≠x | B. | ?x∈R,x2≠x | C. | ?x∉R,x2≠x | D. | ?x∈R,x2≠x |
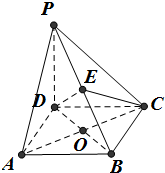 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2${\sqrt{3}^{\;}}$,且AC,BD交于点O,E是PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2${\sqrt{3}^{\;}}$,且AC,BD交于点O,E是PB上任意一点.