题目内容
13．空间四边形ABCD中，E、F分别为AC、BD中点，若CD=2AB=2，EF⊥AB，则EF与CD所成的角为（ ）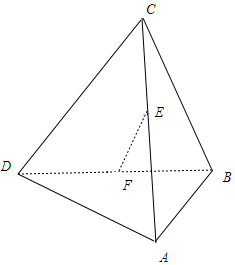
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 取AD的中点G，连接EG、FG，由三角形中位线定理得EG∥CD，从而得到∠GEF是EF与CD所成的角，由此能求出EF与CD所成的角的大小．
解答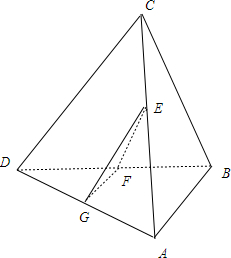 
解：取AD的中点G，连接EG、FG，
∵E、F分别为AC、BD中点，
∴EG∥CD，且EG=$\frac{1}{2}CD$=1，
FG∥AB，且FG=$\frac{1}{2}AB$=$\frac{1}{2}$．
∵EF⊥AB，FG∥AB，∴EF⊥FG．
∵EG∥CD，∴∠GEF是EF与CD所成的角，
在Rt△EFG中，∵EG=1，GF=$\frac{1}{2}$，EF⊥FG，∴∠GEF=30°，
即EF与CD所成的角为30°．
故选：A．
点评 本题考查的知识点是异面直线及其所成的角，理解异面直线夹角的定义利用平移法，构造出满足条件的平面角是解答的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．函数f（x）=$\frac{{\sqrt{1-{x^2}}}}{x}$的定义域为（ ）
| A． | [-1，0）∪（0，1] | B． | [-1，1] | C． | [-1，0）∪（0，1） | D． | [-1，1） |
1．已知集合A={x|x≥a}，B={x|1≤x＜2}，且A∪∁RB=R，则实数a的取值范围是（ ）
| A． | （-∞，1] | B． | （-∞，1） | C． | [2，+∞） | D． | （2，+∞） |
18．设函数f（x）=sin（ωx+φ），A＞0，ω＞0，若f（x）在区间[$\frac{π}{6}$，$\frac{π}{2}$]上单调，且f（$\frac{π}{2}$）=f（$\frac{2π}{3}$）=-f（$\frac{π}{6}$），则f（x）的最小正周期为 （ ）
| A． | $\frac{π}{2}$ | B． | 2π | C． | 4π | D． | π |
5．为了得到函数y=$\sqrt{2}$cos3x的图象，可以将函数y=sin3x+cos3x的图象（ ）
| A． | 向右平移$\frac{π}{4}$个单位 | B． | 向左平移$\frac{π}{4}$个单位 | ||
| C． | 向右平移$\frac{π}{12}$个单位 | D． | 向左平移$\frac{π}{12}$个单位 |
2．已知函数f（x）是定义在R上的偶函数，若对任意x∈R，都有f（4+x）=f（-x），且当x∈[0，2]时，f（x）=2x-1，则下列结论不正确的是（ ）
| A． | 函数f（x）的最小正周期为4 | B． | f（1）＜f（3） | ||
| C． | f（2016）=0 | D． | 函数f（x）在区间[-6，-4]上单调递减 |