题目内容
8.已知双曲线$\frac{x^2}{3}-\frac{y^2}{m}=1({m>0})$的离心率为e,经过第一、三象限的渐近线的斜率为k,且e≥$\sqrt{2}$k.(1)求m的取值范围;
(2)设条件p:e≥$\sqrt{2}$k;条件q:m2-(2a+2)m+a(a+2)≤0.若p是q的必要不充分条件,求a的取值范围.
分析 (1)由已知得:$e=\frac{{\sqrt{4+m}}}{{\sqrt{3}}}$,$k=\frac{{\sqrt{m}}}{{\sqrt{3}}}$,利用e≥$\sqrt{2}$k,m>0,即可求m的取值范围;
(2)求出q的等价结论,利用p是q的必要不充分条件,求a的取值范围.
解答 解:(1)由已知得:$e=\frac{{\sqrt{4+m}}}{{\sqrt{3}}}$,$k=\frac{{\sqrt{m}}}{{\sqrt{3}}}$,
∵$e≥\sqrt{2}k$,∴$\frac{{\sqrt{3+m}}}{{\sqrt{3}}}≥\sqrt{2}•\frac{{\sqrt{m}}}{{\sqrt{3}}}$,解得m≤3,
∵m>0,∴0<m≤3,即m的取值范围(0,3].
(2)∵m2-(2a+2)m+a(a+2)≤0,∴(m-a)(m-a-2)≤0,即a≤m≤a+2,
∵p是q的必要不充分条件,∴$\left\{\begin{array}{l}a>0\\ a+2≤3\end{array}\right.$
解得0<a≤1,即a的取值范围为(0,1].
点评 本题考查双曲线的方程与性质,考查充要条件,知识综合性强.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
13.某程序框图如图所示,若该程序运行后输出的值是$\frac{25}{13}$,则( )
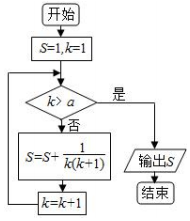

| A. | a=11 | B. | a=12 | C. | a=13 | D. | a=14 |
20.执行图中程序框图,若输入x1=2,x2=3,x3=7,则输出的T值为( )
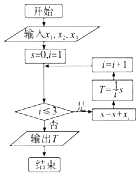

| A. | 3 | B. | 4 | C. | $\frac{11}{3}$ | D. | 5 |
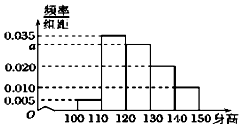 从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).
从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).