题目内容
为了解某班学生喜爱打篮球是否与性别有关,对本班 人进行了问卷调查得到了如下的列联表:
人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
已知在全部
 人中随机抽取1人抽到喜爱打篮球的学生的概率为
人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否认为喜爱打篮球与性别有关?说明你的理由.(参考公式:
 ,其中
,其中 )
)
(1)列联表如下: 喜爱打篮球 不喜爱打篮球 合计 男生 20 5 25 女生 10 15 25 合计 30 20 50
(2)有99%的把握认为喜爱打篮球与性别有关.
解析试题分析:(1)根据在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率,求出喜爱打篮球的人数,进而求出男生的人数,填好表格;(2)根据所给的公式,代入数据求出观测值,把求得的结果与临界值进行比较,看出有多大的把握说明打篮球和性别有关系.
(1) 因为在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 ,所以喜爱打篮球的总人数为
,所以喜爱打篮球的总人数为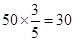 人,所以列联表补充如下:
人,所以列联表补充如下:
4分 喜爱打篮球 不喜爱打篮球 合计 男生 20 5 25 女生 10 15 25 合计 30 20 50
(2)根据列联表可得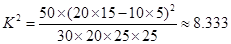
因为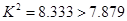 10分
10分
∴有99%以上的把握认为喜爱打篮球与性别有关 12分.
考点:独立性检验.

练习册系列答案
相关题目
某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
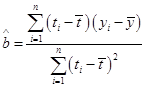 ,
,
某网站针对“2014年法定节假日调休安排”展开的问卷调查,提出了A、B、C三种放假方案,调查结果如下:
| | 支持A方案 | 支持B方案 | 支持C方案 |
| 35岁以下 | 200 | 400 | 800 |
| 35岁以上(含35岁) | 100 | 100 | 400 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持A方案”的人中抽取了6人,求n的值;
(2)在“支持B方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率.
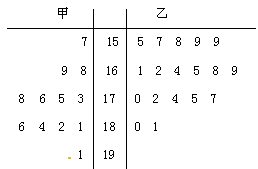
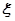 的分布列。
的分布列。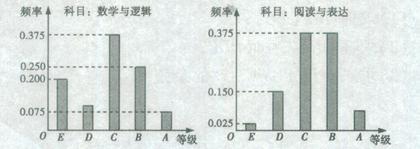
 元/张
元/张 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
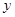 (万元)和房屋的面积
(万元)和房屋的面积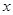 (
( )的数据 ,若由资料可知
)的数据 ,若由资料可知
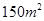 时的销售价格.
时的销售价格.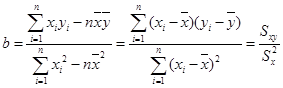
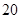 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于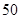 公里和
公里和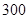 公里之间,将统计结果分
公里之间,将统计结果分 组:
组: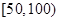 ,
,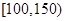 ,
,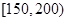 ,
,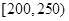 ,
, ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
 的值;
的值;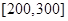 的车辆数;
的车辆数;