题目内容
电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”, 并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”.
(1)试估算该市“足球迷”的人数,并指出其中“铁杆足球迷”约为多少人;
(2)该市要举办一场足球比赛,已知该市的足球场可容纳10万名观众.根据调查,如果票价定为100元/张,则非“足球迷”均不会到现场观看,而“足球迷”均愿意前往现场观看.如果票价提高 元/张
元/张 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
(1)16万“足球迷”, 3万“铁杆足球迷”,(2)140元/张
解析试题分析:(1)利用频数等于频率乘以总数,样本中“足球迷”出现的频率=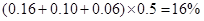 “足球迷”的人数=
“足球迷”的人数= ,同理可求:“铁杆足球迷”=
,同理可求:“铁杆足球迷”= ,(2)如果票价定为100元/张,则非“足球迷”均不会到现场观看,而“足球迷”均愿意前往现场观看,现场观看足球比赛的人数超过10万人,所以设票价为
,(2)如果票价定为100元/张,则非“足球迷”均不会到现场观看,而“足球迷”均愿意前往现场观看,现场观看足球比赛的人数超过10万人,所以设票价为 元,则一般“足球迷”中约有
元,则一般“足球迷”中约有 万人,“铁杆足球迷”约有
万人,“铁杆足球迷”约有 万人去现场看球. 由
万人去现场看球. 由 得
得 由
由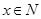 ,
, 即平均票价至少定为100+40=140元,才能使前往现场观看足球比赛的“足球迷”不超过10万人.
即平均票价至少定为100+40=140元,才能使前往现场观看足球比赛的“足球迷”不超过10万人.
(1)样本中“足球迷”出现的频率=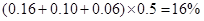 (2分)
(2分)
“足球迷”的人数= (万) (2分)
(万) (2分)
“铁杆足球迷”= (万)
(万)
所以16万“足球迷”中,“铁杆足球迷”约有3万人. (6分)
(2)设票价为 元,则一般“足球迷”中约有
元,则一般“足球迷”中约有 万人,“铁杆足球迷”约有
万人,“铁杆足球迷”约有 万人去现场看球. (3分)
万人去现场看球. (3分)
令 (5分)
(5分)
化简得:
解得: ,由
,由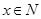 ,
, (7分)
(7分)
即平均票价至少定为100+40=140元,才能使前往现场观看足球比赛的“足球迷”不超过10万人. (8分)
考点:频率分布直方图

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案对某校小学生进行心理障碍测试得到如下的列联表:
| | 有心理障碍 | 没有心理障碍 | 总计 |
| 女生 | 10 | | 30 |
| 男生 | | 70 | 80 |
| 总计 | 20 | | 110 |
将表格填写完整,试说明心理障碍与性别是否有关?
附:

| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |

(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
为了解某班学生喜爱打篮球是否与性别有关,对本班 人进行了问卷调查得到了如下的列联表:
人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
已知在全部
 人中随机抽取1人抽到喜爱打篮球的学生的概率为
人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否认为喜爱打篮球与性别有关?说明你的理由.(参考公式:
 ,其中
,其中 )
) 甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个 的列联表;(2)试判断成绩与班级是否有关?
的列联表;(2)试判断成绩与班级是否有关?
参考公式: ;
;
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
为调查民营企业的经营状况,某统计机构用分层抽样的方法从A、B、C三个城市中,抽取若干个民营企业组成样本进行深入研究,有关数据见下表:(单位:个)
| 城市 | 民营企业数量 | 抽取数量 |
| A |  | 4 |
| B | 28 |  |
| C | 84 | 6 |
(1)求
 、
、 的值;
的值;(2)若从城市A与B抽取的民营企业中再随机选2个进行跟踪式调研,求这2个都来自城市A的概率.
某校高三年级一次数学考试后,为了解学生的数学学习情况,随机抽取 名学生的数学成绩,制成表所示的频率分布表.
名学生的数学成绩,制成表所示的频率分布表.
| 组号 | 分组 | 频数 | 频率 |
| 第一组 |  |  |  |
| 第二组 |  |  |  |
| 第三组 |  |  |  |
| 第四组 |  | 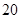 |  |
| 第五组 |  |  |  |
| 合计 |  |  | |
 、
、 、
、 的值;
的值;(2)若从第三、四、五组中用分层抽样方法抽取
 名学生,并在这
名学生,并在这 名学生中随机抽取
名学生中随机抽取 名学生与张老师面谈,求第三组中至少有
名学生与张老师面谈,求第三组中至少有 名学生与张老师面谈的概率
名学生与张老师面谈的概率 
 和样本方差
和样本方差 (同一组的数据用该组区间的中点值作代表);
(同一组的数据用该组区间的中点值作代表); 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 近似为样本方差
近似为样本方差 ;
; 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间 的产品件数.利用(i)的结果,求
的产品件数.利用(i)的结果,求 .
.
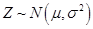 则
则 ,
, 。
。 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 的学生人数为6.
的学生人数为6. 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在