题目内容
以下是某地搜集到的新房屋的销售价格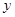 (万元)和房屋的面积
(万元)和房屋的面积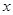 (
( )的数据 ,若由资料可知
)的数据 ,若由资料可知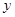 对
对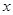 呈线性相关关系。
呈线性相关关系。
试求:(1)线性回归方程;
(2)根据(1)的结果估计当房屋面积为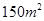 时的销售价格.
时的销售价格.
参考公式: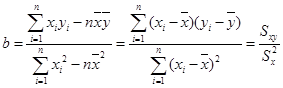
(1) (2)105
(2)105
解析试题分析:(1)根据数据表先求 ,再根据公式求
,再根据公式求 ,根据线性回归直线必过样本中心点
,根据线性回归直线必过样本中心点 ,可得
,可得 。(2)将
。(2)将 代入回归方程即可得所求。
代入回归方程即可得所求。
解:(1)由已知数据表求得: , 2分
, 2分
将数据代入 计算得:b=0.84, 6分
计算得:b=0.84, 6分
又由 得:
得: 8分
8分
线性回归方程为: . 9分
. 9分
(2)当 时,求得
时,求得 (万元), 12分
(万元), 12分
所以当房屋面积为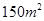 时的销售价格为105万元。 13分
时的销售价格为105万元。 13分
考点:线性回归方程。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
高中流行这样一句话“文科就怕数学不好,理科就怕英语不好”.下
表是一次针对高三文科学生的调查所得的数据,试问:在出错概率不超过0.01的前提下文
科学生总成绩不好与数学成绩不好有关系吗?
| | 总成绩好 | 总成绩不好 | 总计 |
| 数学成绩好 | 20 | 10 | 30 |
| 数学成绩不好 | 5 | 15 | 20 |
| 总计 | 25 | 25 | 50 |
(P(K2≥3.841)≈0.05,P(K2≥6.635)≈0.01)
为了解某班学生喜爱打篮球是否与性别有关,对本班 人进行了问卷调查得到了如下的列联表:
人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
已知在全部
 人中随机抽取1人抽到喜爱打篮球的学生的概率为
人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否认为喜爱打篮球与性别有关?说明你的理由.(参考公式:
 ,其中
,其中 )
) (13分)(2011•广东)在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
为调查民营企业的经营状况,某统计机构用分层抽样的方法从A、B、C三个城市中,抽取若干个民营企业组成样本进行深入研究,有关数据见下表:(单位:个)
| 城市 | 民营企业数量 | 抽取数量 |
| A |  | 4 |
| B | 28 |  |
| C | 84 | 6 |
(1)求
 、
、 的值;
的值;(2)若从城市A与B抽取的民营企业中再随机选2个进行跟踪式调研,求这2个都来自城市A的概率.
(2014·泰安模拟)某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示:
| 锻炼时间 (分钟) | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120) |
| 人数 | 40 | 60 | 80 | 100 | 80 | 40 |
(1)其中课外体育锻炼时间在
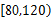 分钟内的学生应抽取多少人?
分钟内的学生应抽取多少人?(2)若从(1)中被抽取的学生中随机抽取2名,求这2名学生课外体育锻炼时间均在
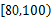 分钟内的概率.
分钟内的概率. 关于某设备的使用年限 和所支出的维修费用
和所支出的维修费用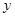 (万元),有如下的统计资料:
(万元),有如下的统计资料:
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
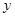 对
对 呈线形相关关系.试求:线形回归方程;(
呈线形相关关系.试求:线形回归方程;( ,
, )
)(2)估计使用年限为10年时,维修费用是多少?
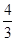 倍.
倍.
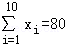 ,
, ,
, ,
,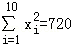 .
. ,
,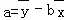 ,其中
,其中 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为 .
.