题目内容
设
=2
-
+
,
=
+3
-2
,
=-2
+
-3
,
=3
+2
+5
,(其中
,
,
是两两垂直的单位向量),若
=λ
+μ
+ν
,则实数λ,μ,ν的值分别是( )
| a1 |
| m |
| j |
| k |
| a2 |
| m |
| j |
| k |
| a3 |
| m |
| j |
| k |
| a4 |
| m |
| j |
| k |
| m |
| j |
| k |
| a4 |
| a1 |
| a2 |
| a3 |
| A、1,-2,-3 |
| B、-2,1,-3 |
| C、-2,1,3 |
| D、-1,2,3 |
考点:向量的数量积判断向量的共线与垂直
专题:平面向量及应用
分析:利用向量的线性运算、向量相等即可得出.
解答:
解:∵
=λ
+μ
+ν
,
∴3
+2
+5
=λ(2
-
+
)+μ(
+3
-2
)+v(-2
+
-3
)=(2λ+μ-2v)
+(-λ+3μ+v)
+(λ-2μ-3v)
,
∴
,解得
.
故选:B.
| a4 |
| a1 |
| a2 |
| a3 |
∴3
| m |
| j |
| k |
| m |
| j |
| k |
| m |
| j |
| k |
| m |
| j |
| k |
| m |
| j |
| k |
∴
|
|
故选:B.
点评:本题考查了向量的线性运算、向量相等,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
空间4点A,B,C,D共面但不共线,下列结论中正确的是( )
| A、4点中必能找出其中3点共线 |
| B、4点中必能找出其中3点不共线 |
| C、AB,BC,CD,DA中必有两条平行 |
| D、AB与CD必相交 |
若圆C的半径为1,点C与点(2,0)关于点(1,0)对称,则圆C的标准方程为( )
| A、x2+y2=1 |
| B、(x-3)2+y2=1 |
| C、(x-1)2+y2=1 |
| D、x2+(y-3)2=1 |
下列程序运行后的输出结果为( )


| A、12 | B、36 | C、48 | D、144 |
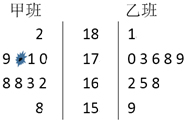 随机抽取某中学高三年级甲乙两班各10名同学,测量出他们的身高(单位:cm),获得身高数据的茎叶图如图.其中甲班有一个数据被污损.
随机抽取某中学高三年级甲乙两班各10名同学,测量出他们的身高(单位:cm),获得身高数据的茎叶图如图.其中甲班有一个数据被污损. 在如图所示的茎叶图中,甲、乙两组数据的中位数分别是
在如图所示的茎叶图中,甲、乙两组数据的中位数分别是