Question

【题目】已知a＞0，b＞0，函数f（x）＝｜x＋a｜＋｜2x－b｜的最小值为1．

（1）证明：2a＋b＝2；

（2）若a＋2b≥tab恒成立，求实数t的最大值．

Answer 1

【答案】（1）证明： ，

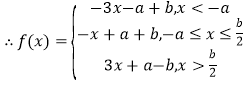显然f(x)在上单调递减，在上单调递增，

所以f(x)的最小值为f＝a＋＝1，即2a＋b＝2.；

（2）

【解析】

（1）绝对值不等式，根据各个绝对值的零点进行分段化简，由函数的单调性求出最值，列出等式，即可证得结论；

（2）恒成立问题分离参数，结合第一问的结论，利用基本不等式，即可得到结果.

（1）证明：

，

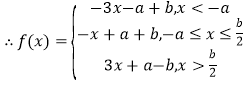显然f(x)在上单调递减，在上单调递增，

所以f(x)的最小值为f＝a＋＝1，即2a＋b＝2.

（2）因为a＋2b≥tab恒成立，所以恒成立，

＝＋＝ (2a＋b)＝ ≥，

当且仅当a＝b＝时，取得最小值.

所以t≤，即实数t的最大值为.