题目内容
3.双曲线$\frac{x^2}{5}-\frac{y^2}{4}=1$的离心率为( )| A. | 4 | B. | $\frac{{3\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{3}{2}$ |
分析 通过双曲线方程求出a,b,c的值然后求出离心率即可.
解答 解:因为双曲线$\frac{x^2}{5}-\frac{y^2}{4}=1$,所以a=$\sqrt{5}$,b=2,所以c=3,
所以双曲线的离心率为:e=$\frac{c}{a}$=$\frac{3\sqrt{5}}{5}$.
故选B.
点评 本题考查双曲线的基本性质的应用,离心率的求法,考查计算能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
14.设函数$f(x)=\frac{{6sinxcosx-4cosx{{sin}^3}x}}{{2\sqrt{2}+sin(2x+\frac{π}{4})+cos(2x+\frac{π}{4})}}$,则( )
| A. | y=f(x)是偶函数,在$(0,\frac{π}{2})$上单调递增 | B. | y=f(x)是奇函数,在$(0,\frac{π}{4})$上单调递增 | ||
| C. | y=f(x)是偶函数,在$(0,\frac{π}{2})$上单调递减 | D. | y=f(x)是奇函数,在$(0,\frac{π}{4})$上单调递减 |
8.已知曲线C1:y2=tx (y>0,t>0)在点M($\frac{4}{t}$,2)处的切线与曲线C2:y=ex+l-1也相切,则t的值为( )
| A. | 4e2 | B. | 4e | C. | $\frac{e^x}{4}$ | D. | $\frac{e}{4}$ |
15.若${(a+i)^2}-\frac{1}{i}∈R(a∈R,i$是虚数单位),则a=( )
| A. | 1 | B. | 0 | C. | 一$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
6.如图是f(x)=$\frac{{2\sqrt{3}}}{3}$cos(ωx+φ)(ω>0)的部分图象,下列说法错误的是( )
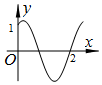
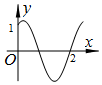
| A. | 函数f(x)的最小正周期是$\frac{12}{5}$ | |
| B. | 函数g(x)=$\frac{{2\sqrt{3}}}{3}sin\frac{5π}{6}$x的图象可由函数f(x)的图象向右平移$\frac{2}{5}$个单位得到 | |
| C. | 函数f(x)图象的一个对称中心是(-$\frac{4}{5}$,0) | |
| D. | 函数f(x)的一个递减区间是(5,$\frac{31}{5}$) |
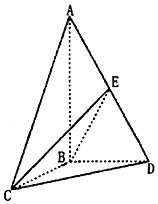 如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.
如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.