题目内容
19.设A,B分别是直线y=$\frac{2\sqrt{5}}{5}$x和y=-$\frac{2\sqrt{5}}{5}$x上的两个动点,并且|$\overrightarrow{AB}$|=$\sqrt{20}$,动点P满足$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$,记动点P的轨迹为C,求轨迹C的方程是$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$.分析 设动点P(x,y),再由题意设出A、B的坐标,根据$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$,列出坐标之间的关系,再由|$\overrightarrow{AB}$|=$\sqrt{20}$,向量模的公式,列出关于x和y的关系式,化简后得到所求的轨迹方程.
解答 解:设P(x,y),
由题可令A(x1,$\frac{2\sqrt{5}}{5}$x1),B(x2,$\frac{2\sqrt{5}}{5}$x2),
∵$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$,
∴$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=x}\\{{x}_{1}-{x}_{2}=\frac{\sqrt{5}}{2}y}\end{array}\right.$
又∵|$\overrightarrow{AB}$|=$\sqrt{20}$,
∴(x1-x2)2+$\frac{4}{5}$(x1+x2)2=20.
∴轨迹C的方程为$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$.
故答案为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$.
点评 本题主要考查了求轨迹方程,解题的前提是要求学生对基础知识有相当熟练的把握.

练习册系列答案
相关题目
20.5弧度的角的终边所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.已知等比数列{an}中,a1+a2=10,a3+a4=40,则a5+a6=( )
| A. | 20 | B. | 40 | C. | 160 | D. | 320 |
4.若直线l:xsinθ+2ycosθ=1与圆C:x2+y2=1相切,则直线l的方程为( )
| A. | x=1 | B. | x=±1 | C. | y=1 | D. | y=±1 |
9.已知集合A={x|-1<x<4},B={x|-2<x<3},则A∩B=( )
| A. | {x|-1<x<3} | B. | {x|0≤x≤2} | C. | {0,1,2} | D. | {0,1,2,3} |
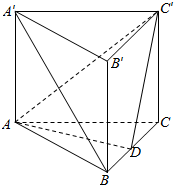 如图,三棱柱ABC-A′B′C′中,侧棱AA′⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点
如图,三棱柱ABC-A′B′C′中,侧棱AA′⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点