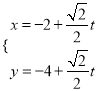题目内容
【题目】正方体ABCD - A1B1C1D1的棱长为2, E、F、G分别为BC、CC1、BB1的中点,则( )
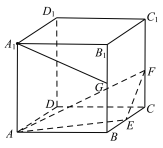
A.直线![]() 与直线AF垂直B.直线A1G与平面AEF平行
与直线AF垂直B.直线A1G与平面AEF平行
C.平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]() D.点C与点G到平面AEF的距离相等
D.点C与点G到平面AEF的距离相等
【答案】BC
【解析】
对选项A,取![]() 中点
中点![]() ,则
,则![]() 为
为![]() 在平面
在平面![]() 上的投影,由
上的投影,由![]() 与
与![]() 不垂直,得
不垂直,得![]() 与
与![]() 不垂直,故A错误.对选项B,取
不垂直,故A错误.对选项B,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,易证平面
,易证平面![]() 平面
平面![]() ,从而得到
,从而得到![]() 平面
平面![]() ,故B正确.对选项C,连接
,故B正确.对选项C,连接![]() ,
,![]() ,得到
,得到
平面![]() 为平面
为平面![]() 截正方体所得的截面,再计算其面积即可得到C正确,对选项D,利用反正法即可得到D错误.
截正方体所得的截面,再计算其面积即可得到C正确,对选项D,利用反正法即可得到D错误.
对选项A,如图所示:
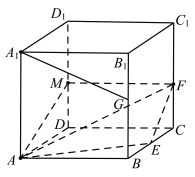
取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() .
.
则![]() 为
为![]() 在平面
在平面![]() 上的投影,
上的投影,
因为![]() 与
与![]() 不垂直,所以
不垂直,所以![]() 与
与![]() 不垂直,故A错误.
不垂直,故A错误.
对选项B,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,如图所示:
,如图所示:
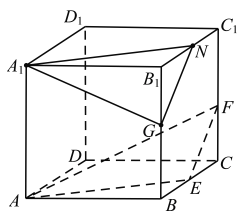
因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故B正确.
,故B正确.
对选项C,连接![]() ,
,![]() ,如图所示:
,如图所示:
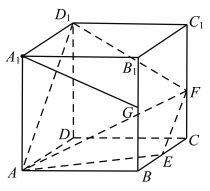
因为![]() ,所以平面
,所以平面![]() 为平面
为平面![]() 截正方体所得的截面.
截正方体所得的截面.
![]() ,
,![]() ,
,
![]() ,所以四边形
,所以四边形![]() 为等腰梯形,
为等腰梯形,
高为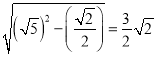 ,
,![]() .
.
故C正确.
对选项D,连接![]() 交
交![]() 于
于![]() ,如图所示:
,如图所示:
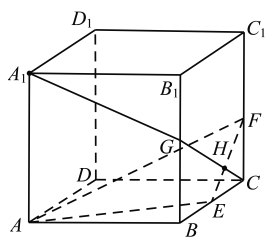
假设点![]() 与点
与点![]() 到平面
到平面![]() 的距离相等,即平面
的距离相等,即平面![]() 必过
必过![]() 的中点,
的中点,
而![]() 不是
不是![]() 的中点,则假设不成立,故D错误.
的中点,则假设不成立,故D错误.
故选:BC

练习册系列答案
相关题目