题目内容
2.直线y=-x+b与曲线$y=\sqrt{4-{x^2}}$有且只有两个公共点,则b的取值范围是( )| A. | 2<b<2$\sqrt{2}$ | B. | 2≤b<2$\sqrt{2}$ | C. | 2≤b≤2$\sqrt{2}$ | D. | 2<b≤2$\sqrt{2}$ |
分析 由曲线$y=\sqrt{4-{x^2}}$变形为x2+y2=4(y≥0),画出y=-x+b,x2+y2=4(y≥0)图象.当直线经过点(2,0),(0,2)时,直线与曲线有两个公共点,求出此时b.再求出当直线与曲线相切时b的值即可.
解答  解:由曲线$y=\sqrt{4-{x^2}}$变形为x2+y2=4(y≥0)
解:由曲线$y=\sqrt{4-{x^2}}$变形为x2+y2=4(y≥0)
画出y=-x+b,x2+y2=4(y≥0)图象,
①当直线经过点(2,0),(0,2)时,直线与曲线有两个公共点,此时b=2.
②当直线与曲线相切时,联立直线y=-x+b与曲线$y=\sqrt{4-{x^2}}$,
化为2x2+2bx+b2-4=0,令△=4b2-8(b2-4)=0,解得b=2$\sqrt{2}$.
因此,当2≤b<2$\sqrt{2}$时,直线与曲线有两个公共点.
∴b的取值范围是2≤b<2$\sqrt{2}$.
故选:B.
点评 本题考查了有条件的直线与圆相交相切问题、数形结合等基础知识与基本技能方法,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
10.(理科)cos43°cos77°+sin43°cos167°=-$\frac{1}{2}$.
(文科)sin43°cos77°+cos43°sin77°=$\frac{\sqrt{3}}{2}$.
(文科)sin43°cos77°+cos43°sin77°=$\frac{\sqrt{3}}{2}$.
7.在数列{an}中,a1=1,anan-1=an-1+(-1)n(n≥2,n∈N*),则$\frac{a_3}{a_4}$的值是( )
| A. | $\frac{15}{16}$ | B. | $\frac{15}{8}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{8}$ |
14.设a>0,b>0,e是自然对数的底数)以下命题正确的为( )
| A. | 若ea+2a=eb+3b,则a>b | B. | 若ea+2a=eb+3b,则a<b | ||
| C. | 若ea-2a=eb-3b,则a>b | D. | 若ea-2a=eb-3b,则a<b |
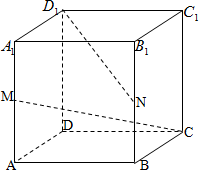 正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.求:
正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.求: