题目内容
已知a，b，c为互不相等的非负数．求证：a2+b2+c2＞
（
+
+
）．
| abc |
| a |
| b |
| c |
考点：不等式的证明
专题：证明题,不等式的解法及应用
分析：a，b，c为互不相等的非负数，利用基本不等式，即可得出结论．
解答：
证明：∵a，b，c是正数，
∴a2+b2≥2ab，b2+c2≥2bc，c2+a2≥2ac；
又a，b，c是不全相等的正数，
∴等号不能同时取．
∴a2+b2+c2＞ab+bc+ca，
∵ab+bc≥2
，bc+ac≥2
，ab+ac≥2
，
又a，b，c是不全相等的正数，
∴ab+bc+ca＞
（
+
+
）．
∴a2+b2+c2＞
（
+
+
）．
∴a2+b2≥2ab，b2+c2≥2bc，c2+a2≥2ac；
又a，b，c是不全相等的正数，
∴等号不能同时取．
∴a2+b2+c2＞ab+bc+ca，
∵ab+bc≥2
| ab2c |
| abc2 |
| a2bc |
又a，b，c是不全相等的正数，
∴ab+bc+ca＞
| abc |
| a |
| b |
| c |
∴a2+b2+c2＞
| abc |
| a |
| b |
| c |
点评：本题考查不等式的证明，着重考查基本不等式的应用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
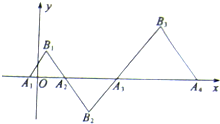如图，在直角坐标平面xOy中，△AjBjAj+1（其中j=1，2，n，…）为正三角形，且满足