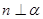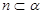题目内容
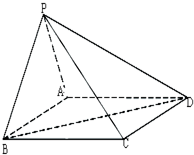
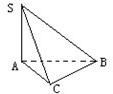
如图,在四棱锥P-ABCD中,底面ABCD是矩形,知AB=3,AD=2,PA=2,PD=2
,∠PAB=60°.
(1)证明:AD⊥平面PAB;
(2)求异面直线PC与AD所成的角的余弦值;
(3)求二面角P-BD-A的大小余弦值.
| 2 |
(1)证明:AD⊥平面PAB;
(2)求异面直线PC与AD所成的角的余弦值;
(3)求二面角P-BD-A的大小余弦值.

(1)证明:在△PAD中,由题设PA=2,PD=2
,
可得PA2+AD2=PD2,于是AD⊥PA;
在矩形ABCD中,AD⊥AB,
又PA∩AB=A,所以AD⊥平面PAB;
(2)由题意得,BC∥AD,所以∠PCB(或其补角)是异面直线PC与AD所成的角
在△PAB中,由余弦定理得PB=
=
由(1)知AD⊥平面PAB,
∵PB?平面PAB,∴AD⊥PB,∴BC⊥PB,
故△PBC是直角三角形,
∴tan∠PCB=
=
,
∴异面直线PC与AD所成的角的余弦值为
;
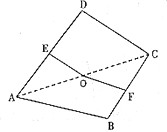
(3)过点P作PH⊥AB于H,过H作HE⊥BD于E,连接PE
∵AD⊥平面PAB,PH?平面PAB,
∴AD⊥PH
∵AD∩AB=A
∴PH⊥平面ABCD
∴∠PEH为二面角P-BD-A的平面角
∵PH=PAsin60°=
,AH=PAcos60°=1
∴BH=AB-AH=2,BD=
=
∴HE=
•BH=
在直角△PHE中,tan∠PEH=
∴二面角P-BD-A的余弦值为
.

| 2 |
可得PA2+AD2=PD2,于是AD⊥PA;
在矩形ABCD中,AD⊥AB,
又PA∩AB=A,所以AD⊥平面PAB;
(2)由题意得,BC∥AD,所以∠PCB(或其补角)是异面直线PC与AD所成的角
在△PAB中,由余弦定理得PB=
| PA2+AB2-2PA•AB•cos∠PAB |
| 7 |
由(1)知AD⊥平面PAB,
∵PB?平面PAB,∴AD⊥PB,∴BC⊥PB,
故△PBC是直角三角形,
∴tan∠PCB=
| PB |
| BC |
| ||
| 2 |
∴异面直线PC与AD所成的角的余弦值为
2
| ||
| 11 |
(3)过点P作PH⊥AB于H,过H作HE⊥BD于E,连接PE
∵AD⊥平面PAB,PH?平面PAB,
∴AD⊥PH
∵AD∩AB=A
∴PH⊥平面ABCD
∴∠PEH为二面角P-BD-A的平面角
∵PH=PAsin60°=
| 3 |
∴BH=AB-AH=2,BD=
| AB2+AD2 |
| 13 |
∴HE=
| AD |
| BD |
| 4 | ||
|
在直角△PHE中,tan∠PEH=
| ||
| 4 |
∴二面角P-BD-A的余弦值为
4
| ||
| 55 |


练习册系列答案
相关题目

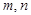 和平面
和平面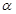 ,则
,则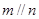 的一个必要条件是( )
的一个必要条件是( )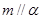 ,
,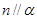
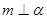 ,
,