题目内容
9.过抛物线y2=4x的焦点作倾斜角α的弦,若弦长不超过8,则α的取值范围是[$\frac{π}{4}$,$\frac{3π}{4}$].分析 讨论直线是否有斜率,联立方程组,利用焦点弦公式和根与系数的关系得出不等式解出斜率的范围,即可得出倾斜角的范围.
解答 解:抛物线的准线方程为x=-1,焦点坐标为(1,0),
(1)若过焦点的直线无斜率,则直线方程为x=1,代入y2=4x得y=±2,
此时弦长为4,符合题意.
(2)若过焦点的直线有斜率,设直线方程为y=k(x-1),
联立方程组$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,消去y得k2x2-(2k2+4)x+k2=0,
设直线与抛物线交点为A(x1,y1),B(x2,y2),则x1+x2=$\frac{2{k}^{2}+4}{{k}^{2}}$,
∴|AB|=x1+x2+2=4+$\frac{4}{{k}^{2}}$,
∵|AB|≤8,即4+$\frac{4}{{k}^{2}}$≤8,解得k≥1或k≤-1,
∴$\frac{π}{4}$$≤α<\frac{π}{2}$或$\frac{π}{2}<α≤\frac{3π}{4}$.
综上,$\frac{π}{4}$≤α≤$\frac{3π}{4}$.
故答案为:[$\frac{π}{4}$,$\frac{3π}{4}$].
点评 本题考查了抛物线的性质,直线与抛物线的关系,属于中档题.

练习册系列答案
相关题目
4.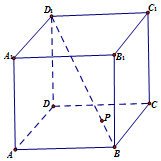 正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,平面α截正方体的表面得到一个多边形,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,当$x∈[{\frac{1}{3},\frac{5}{2}}]$时,函数y=f(x)的值域为( )
正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,平面α截正方体的表面得到一个多边形,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,当$x∈[{\frac{1}{3},\frac{5}{2}}]$时,函数y=f(x)的值域为( )
 正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,平面α截正方体的表面得到一个多边形,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,当$x∈[{\frac{1}{3},\frac{5}{2}}]$时,函数y=f(x)的值域为( )
正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,平面α截正方体的表面得到一个多边形,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,当$x∈[{\frac{1}{3},\frac{5}{2}}]$时,函数y=f(x)的值域为( )| A. | [1,3] | B. | [$\sqrt{6}$,3$\sqrt{6}$] | C. | [$\frac{3\sqrt{6}}{2}$,4$\sqrt{6}$] | D. | [$\sqrt{6}$,4$\sqrt{6}$] |
14.2sin215°-1的值是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
1.下列函数中,最小正周期为π的偶函数是( )
| A. | y=sinx+cosx | B. | y=cos4x-sin4x | C. | y=cos|x| | D. | y=$\frac{tanx}{1-ta{n}^{2}x}$ |
18.8个不同的球放入三个相同的盒子中,问有多少种不同的放法?( )
| A. | 1094 | B. | 966 | C. | 5796 | D. | 6561 |
19.$\frac{sin47°-sin13°}{sin17°}$的值为( )
| A. | $\sqrt{3}$ | B. | 1 | C. | -$\sqrt{3}$ | D. | -1 |
 在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点.
在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点.