题目内容
2.将函数f(x)=sin(ωx+$\frac{π}{6}$)的图象向右平移$\frac{π}{4}$个单位后与g(x)=cos(ωx+$\frac{π}{6}$)的图象重合,则当|ω|最小时,f(π)的值为$\frac{1}{2}$.分析 利用三角函数的图象平移关系,求出|ω|的最小值,结合三角函数的解析式进行求值即可.
解答 解:将函数f(x)=sin(ωx+$\frac{π}{6}$)的图象向右平移$\frac{π}{4}$个单位后,
得y=sin[ω(x-$\frac{π}{4}$)+$\frac{π}{6}$]=sin(ωx+$\frac{π}{6}$-$\frac{π}{4}$ω),
g(x)=cos(ωx+$\frac{π}{6}$)=sin(ωx+$\frac{π}{6}$+$\frac{π}{2}$),
∵平移后的图象重合,
∴$\frac{π}{6}$-$\frac{π}{4}$ω=$\frac{π}{6}$+$\frac{π}{2}$+2kπ,
即-ω=2+8k,
则|ω|=|2+8k|,
则当k=0时,|ω|=2,此时|ω|最小,∴ω=±2
此时f(x)=sin(±2x+$\frac{π}{6}$),
则f(π)=sin(±2π+$\frac{π}{6}$)=sin$\frac{π}{6}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查三角函数解析式的求解,利用三角函数的图象平移关系求出ω的值是解决本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
13.某学校为了提高学生综合素质、树立社会主义荣辱观、发展创新能力和实践能力、促进学生健康成长,开展评选“校园之星”活动.规定各班每10人推选一名候选人,当各班人数除以10的余数大于7时再增选一名候选人,那么,各班可推选候选人人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为( )
| A. | y=[$\frac{x}{10}$] | B. | y=[$\frac{x+2}{10}$] | C. | y=[$\frac{x+3}{10}$] | D. | y=[$\frac{x+4}{10}$] |
17.已知菱形ABCD的边长为2,∠BAD=120°,点E,F分别在边BC,DC上,BE=EC,DF=λDC,若$\overrightarrow{AE}$•$\overrightarrow{AF}$=1,则λ的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
14.已知集合A={x∈N|(x+1)(2-x)≥0},B{y|y=2x,x∈R},则A∩B=( )
| A. | {x|0<x≤2} | B. | {0,1,2} | C. | {1,2} | D. | {1} |
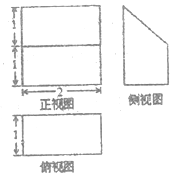
7.某几何体的三视图如图所示,则该几何体的体积等于( )


| A. | 6+6π | B. | 6+8π | C. | 8+6π | D. | 8+8π |