题目内容
9.若a>0,b>0,且$\frac{1}{2a+b}$+$\frac{1}{b+1}$=1,则a+2b的最小值为$\frac{1}{2}$+$\sqrt{3}$.分析 把a+2b变形为a+2b=$\frac{(2a+b)+3(b+1)}{2}$-$\frac{3}{2}$,再利用已知可得a+2b=($\frac{2a+b}{2}$+$\frac{3(b+1)}{2}$)($\frac{1}{2a+b}$+$\frac{1}{b+1}$),利用基本不等式即可得出.
解答 解:∵a>0,b>0,且$\frac{1}{2a+b}$+$\frac{1}{b+1}$=1,
∴a+2b=$\frac{(2a+b)+3(b+1)}{2}$-$\frac{3}{2}$=($\frac{2a+b}{2}$+$\frac{3(b+1)}{2}$)($\frac{1}{2a+b}$+$\frac{1}{b+1}$)-$\frac{3}{2}$=$\frac{1}{2}$+$\frac{2a+b}{2(b+1)}$+$\frac{3(b+1)}{2(2a+b)}$+$\frac{3}{2}$-$\frac{3}{2}$≥$\frac{1}{2}$+2$\sqrt{\frac{2a+b}{2(b+1)}•\frac{3(b+1)}{2(2a+b)}}$=$\frac{1}{2}$+$\sqrt{3}$,
当且仅当$\frac{2a+b}{2(b+1)}$=$\frac{3(b+1)}{2(2a+b)}$,a>0,b>0,且$\frac{1}{2a+b}$+$\frac{1}{b+1}$=1,即b=$\frac{\sqrt{3}}{3}$,a=$\frac{1}{2}$+$\frac{\sqrt{3}}{3}$时,取等号,
∴则a+2b的最小值为$\frac{1}{2}$+$\sqrt{3}$,
故答案为:$\frac{1}{2}$+$\sqrt{3}$.
点评 本题主要考查了不等式的基本性质,恰当变形利用基本不等式是解题的关键.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
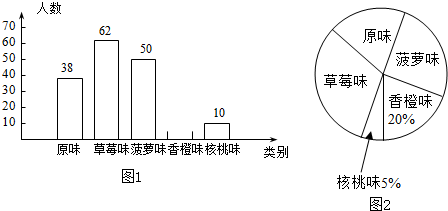
开心蛙口算题卡系列答案(1)根据以上数据完成以下 2×2 列联表:
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
参考公式:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中 n=a+b+c+d.
| P( k2≥k0) | 0.40 | 0.25 | 0.10 | 0.05 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 6.635 |
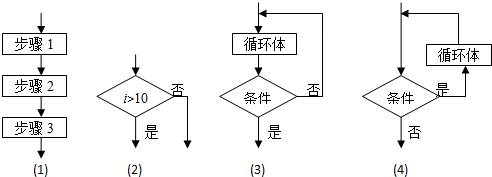
| A. | (1)是顺序结构(2)是条件结构(3)是当型循环结构(4)是直到型循环结构 | |
| B. | (1)是条件结构(2)是顺序结构(3)是当型循环结构(4)是直到型循环结构 | |
| C. | (1)是顺序结构(2)是条件结构(3)是直到型循环结构(4)是当型循环结构 | |
| D. | (1)是顺序结构(2)是当型循环结构(3)是条件结构(4)是直到型循环结构 |
 正三角形ABC的边长为2,将它沿高AD翻折,使BD⊥CD,此时四面体ABCD外接球表面积为5π.
正三角形ABC的边长为2,将它沿高AD翻折,使BD⊥CD,此时四面体ABCD外接球表面积为5π.