题目内容
△ABC中,∠A=60°,∠A的平分线AD交边BC于D,已知AB=3,且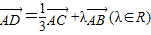 ,则AD的长为( )
,则AD的长为( )A.1
B.
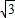
C.
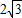
D.3
【答案】分析:作DG∥AB,DH∥AC,证明△ADH≌△ADG,可得AG=DH= AC,根据△BDH∽△BCA,可得BH=
AC,根据△BDH∽△BCA,可得BH= BA=1,从而HA=HD=2,根据等腰三角形知识可求AD的长.
BA=1,从而HA=HD=2,根据等腰三角形知识可求AD的长.
解答: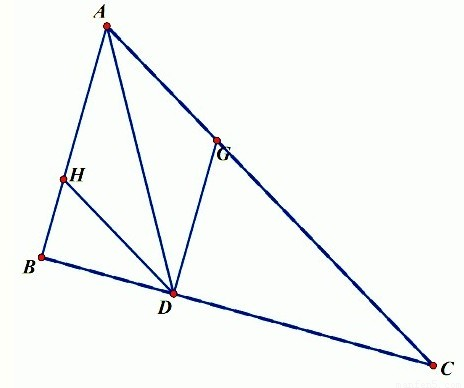 解:如图,作DG∥AB,DH∥AC,则向量
解:如图,作DG∥AB,DH∥AC,则向量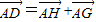 ,∴AG=
,∴AG= AC
AC
因为AD平分∠BAC,所以∠BAD=∠DAC=30°
因为DG∥AB,所以∠ADH=30°=∠DAH,所以AH=DH
同理,AG=DG
∴△ADH≌△ADG
∴AG=DH= AC
AC
又因为△BDH∽△BCA,所以BH= BA=1
BA=1
所以HA=HD=2
根据等腰三角形知识可知AD=2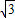
点评:本题考查向量知识的运用,考查三角形的全等与相似,属于中档题.
 AC,根据△BDH∽△BCA,可得BH=
AC,根据△BDH∽△BCA,可得BH= BA=1,从而HA=HD=2,根据等腰三角形知识可求AD的长.
BA=1,从而HA=HD=2,根据等腰三角形知识可求AD的长.解答:
 解:如图,作DG∥AB,DH∥AC,则向量
解:如图,作DG∥AB,DH∥AC,则向量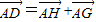 ,∴AG=
,∴AG= AC
AC因为AD平分∠BAC,所以∠BAD=∠DAC=30°
因为DG∥AB,所以∠ADH=30°=∠DAH,所以AH=DH
同理,AG=DG
∴△ADH≌△ADG
∴AG=DH=
 AC
AC又因为△BDH∽△BCA,所以BH=
 BA=1
BA=1所以HA=HD=2
根据等腰三角形知识可知AD=2
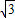
点评:本题考查向量知识的运用,考查三角形的全等与相似,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
△ABC中,a=6,b=6
,A=30°,则边c等于( )
| 3 |
| A、6 | ||
| B、12 | ||
| C、6或12 | ||
D、6
|