题目内容
(本题满分12分)
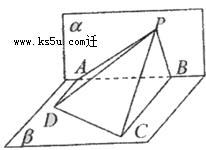
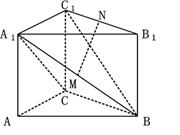
如图,在直三棱柱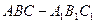 中,
中,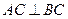 ,
,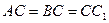 ,
, 是
是 的中点.
的中点.
(Ⅰ)在线段 上是否存在一点
上是否存在一点 ,使得
,使得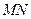 ⊥平面
⊥平面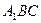 ?若存在,找出点
?若存在,找出点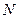 的位置幷证明;若不存在,请说明理由;
的位置幷证明;若不存在,请说明理由;
(Ⅱ)求平面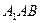 和平面
和平面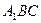 所成角的大小
所成角的大小
如图,在直三棱柱
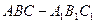 中,
中,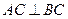 ,
,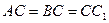 ,
, 是
是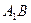 的中点.
的中点.
(Ⅰ)在线段
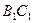 上是否存在一点
上是否存在一点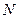 ,使得
,使得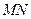 ⊥平面
⊥平面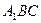 ?若存在,找出点
?若存在,找出点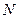 的位置幷证明;若不存在,请说明理由;
的位置幷证明;若不存在,请说明理由;(Ⅱ)求平面
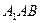 和平面
和平面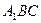 所成角的大小
所成角的大小(Ⅰ)略
(Ⅱ)

解:(Ⅰ)根据题意CA、CB、CC1两两互相垂直
如图:以C为原点, CA、CB、CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系

设AC=BC=CC1=a,则 ,
,
 ,
,
假设在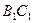 上存在一点N,使
上存在一点N,使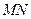 ⊥平面
⊥平面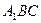 ,设
,设
所以 ,
, ,
,
由 ,
, ,得:
,得:
 N在线段
N在线段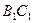 的中点处
的中点处  ---------------------
--------------------- --(6分)
--(6分)
(Ⅱ)由(Ⅰ)知MN⊥平面A1BC,则平面A1BC的一个法向量为 分
分
取AB中点D,连接CD,易证CD⊥平面A1AB
 A1AB的一个法向量
A1AB的一个法向量 -----------------
----------------- -(8分)
-(8分)

所以面 和面
和面 所成的角为
所成的角为 . -----------------(12分)
. -----------------(12分)
如图:以C为原点, CA、CB、CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系

设AC=BC=CC1=a,则
 ,
,
 ,
,假设在
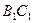 上存在一点N,使
上存在一点N,使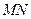 ⊥平面
⊥平面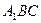 ,设
,设
所以
 ,
, ,
,
由
 ,
, ,得:
,得:
 N在线段
N在线段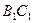 的中点处
的中点处  ---------------------
--------------------- --(6分)
--(6分)(Ⅱ)由(Ⅰ)知MN⊥平面A1BC,则平面A1BC的一个法向量为
 分
分取AB中点D,连接CD,易证CD⊥平面A1AB
 A1AB的一个法向量
A1AB的一个法向量 -----------------
----------------- -(8分)
-(8分)
所以面
 和面
和面 所成的角为
所成的角为 . -----------------(12分)
. -----------------(12分)
练习册系列答案
相关题目
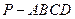 中,侧棱
中,侧棱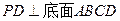 ,底面
,底面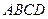 是直角梯形,
是直角梯形,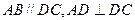 ,且
,且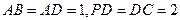 ,
,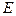 是
是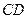 的中点
的中点 .
.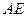 与
与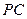 所成的角;
所成的角;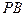
 上是否存在一点
上是否存在一点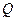 ,使得
,使得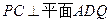 ?若存在,求出
?若存在,求出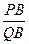 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.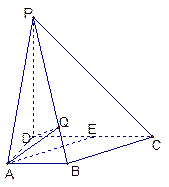
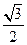 的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA
的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA 1C1C,且A1B=AB=AC=1.
1C1C,且A1B=AB=AC=1.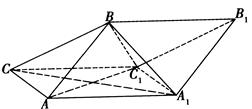
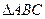 是腰长为2的等腰直角三角形(如图1),
是腰长为2的等腰直角三角形(如图1), ,在边
,在边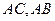 上分别取点
上分别取点 ,使得
,使得 ,把
,把 沿直线
沿直线 折起,使
折起,使 =90°,得四棱锥
=90°,得四棱锥 (如图2).在四棱锥
(如图2).在四棱锥
 (I)求证:CE⊥AF;
(I)求证:CE⊥AF;  时,试在
时,试在 上确定一点G,使得
上确定一点G,使得 ,并证明你的结论.
,并证明你的结论.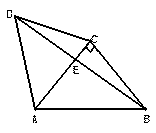
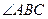 的度数为
的度数为 
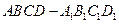 的底面
的底面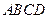 是菱形,
是菱形,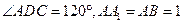 ,点
,点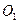 、
、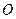 分别是上、下底面菱形的对角线的交点.⑴求证:
分别是上、下底面菱形的对角线的交点.⑴求证: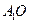 ∥平面
∥平面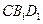 ;⑵求点
;⑵求点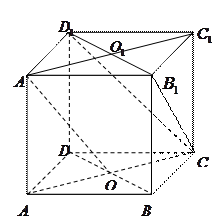
 ,
,
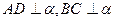 ,AD=4,
,AD=4, ,
,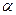 内的轨迹是 ( )
内的轨迹是 ( )