题目内容
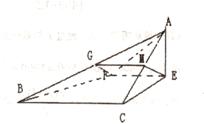
(本小题满分13分)已知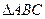 是腰长为2的等腰直角三角形(如图1),
是腰长为2的等腰直角三角形(如图1), ,在边
,在边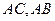 上分别取点
上分别取点 ,使得
,使得 ,把
,把 沿直线
沿直线 折起,使
折起,使 =90°,得四棱锥
=90°,得四棱锥 (如图2).在四棱锥
(如图2).在四棱锥 中,
中,

 (I)求证:CE⊥AF;
(I)求证:CE⊥AF;  (II)当
(II)当 时,试在
时,试在 上确定一点G,使得
上确定一点G,使得 ,并证明你的结论.
,并证明你的结论.





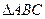 是腰长为2的等腰直角三角形(如图1),
是腰长为2的等腰直角三角形(如图1), ,在边
,在边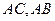 上分别取点
上分别取点 ,使得
,使得 ,把
,把 沿直线
沿直线 折起,使
折起,使 =90°,得四棱锥
=90°,得四棱锥 (如图2).在四棱锥
(如图2).在四棱锥 中,
中,
 (I)求证:CE⊥AF;
(I)求证:CE⊥AF;  (II)当
(II)当 时,试在
时,试在 上确定一点G,使得
上确定一点G,使得 ,并证明你的结论.
,并证明你的结论.




略
解:(Ⅰ)∵△ABC中, ,且
,且 ,∴EF⊥CE
,∴EF⊥CE
又∵ ="90° " ∴CE⊥AE,又∵AE∩EF=E,AE、EF
="90° " ∴CE⊥AE,又∵AE∩EF=E,AE、EF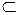 面AEF
面AEF
∴CE⊥面AEF ∵AF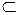 面AEF
面AEF  ∴CE⊥AF………
∴CE⊥AF……… ………………………8分
………………………8分
(Ⅱ)取AB中点G,可得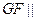 面
面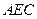 ……………………………9分
……………………………9分
证明如下:取AC中点M,连结GF、EM、GM,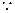
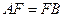
 ,
, G、M分别是AB、AC的中点,
G、M分别是AB、AC的中点, 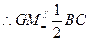 ,
, 
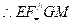 ,
, 四边形
四边形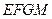 是平行四边形,
是平行四边形,

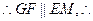
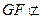 面
面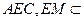 面
面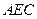 ,
, 
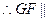 面
面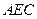 ………13分
………13分
 ,且
,且 ,∴EF⊥CE
,∴EF⊥CE 
又∵
 ="90° " ∴CE⊥AE,又∵AE∩EF=E,AE、EF
="90° " ∴CE⊥AE,又∵AE∩EF=E,AE、EF 面AEF
面AEF∴CE⊥面AEF ∵AF
 面AEF
面AEF  ∴CE⊥AF………
∴CE⊥AF……… ………………………8分
………………………8分(Ⅱ)取AB中点G,可得
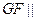 面
面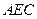 ……………………………9分
……………………………9分证明如下:取AC中点M,连结GF、EM、GM,
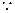
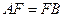
 ,
, G、M分别是AB、AC的中点,
G、M分别是AB、AC的中点, 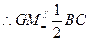 ,
, 
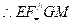 ,
, 四边形
四边形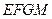 是平行四边形,
是平行四边形, 
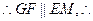
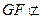 面
面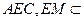 面
面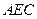 ,
, 
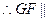 面
面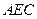 ………13分
………13分
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
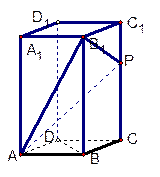
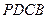 中(如图1),
中(如图1),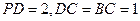 ,
,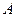 为
为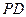 的中点,
的中点,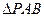 沿
沿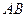 折起,使面
折起,使面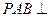 面
面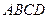 (如图2),点
(如图2),点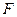 在线段
在线段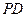 上,
上,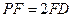 .
.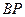 与
与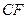 所成角的余弦值;
所成角的余弦值;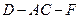 的余弦值;
的余弦值; (3)在四棱锥
(3)在四棱锥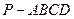 的棱
的棱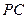 上是否存在一点
上是否存在一点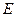 ,使得
,使得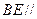 平面
平面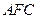 ,若存在,求出
,若存在,求出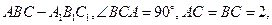
 在底面
在底面 上的射影恰为
上的射影恰为 的中点
的中点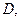 又知
又知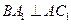 ;
;
 :
: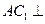 平面
平面 ;
;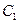 到平面
到平面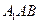 的距离;
的距离;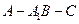 的余弦值;
的余弦值;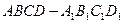 中,
中,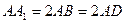 ,且
,且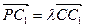
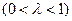 .
.
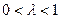 ,总有
,总有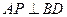 ;
;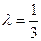 ,求二
,求二 面角
面角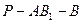 的余弦值;
的余弦值;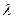 ,使得
,使得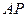 在平面
在平面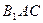 上的射影平分
上的射影平分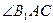 ?若存在,求出
?若存在,求出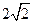 , E、F、G分别为AD、PC、PD的中点.
, E、F、G分别为AD、PC、PD的中点.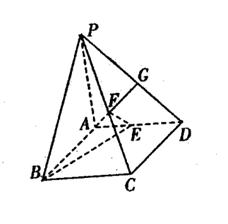
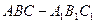 中,
中,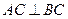 ,
,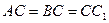 ,
, 是
是 的中点.
的中点.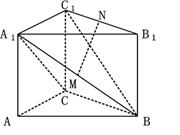
 上是否存在一点
上是否存在一点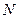 ,使得
,使得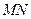 ⊥平面
⊥平面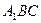 ?若存在,找出点
?若存在,找出点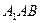 和平面
和平面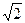 ,CD=1.
,CD=1.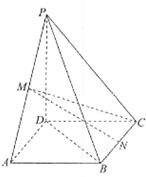
 中,既与
中,既与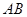 共面也与
共面也与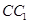 共面的棱的条数为 ( )
共面的棱的条数为 ( )