题目内容
(本小题满分12分)
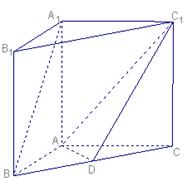
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为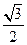 的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA
的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA 1C1C,且A1B=AB=AC=1.
1C1C,且A1B=AB=AC=1.
(1) 求证:AA1⊥BC1;
求证:AA1⊥BC1;
(2) 求三棱锥A1-ABC的体积.
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为
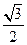 的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA
的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA 1C1C,且A1B=AB=AC=1.
1C1C,且A1B=AB=AC=1.
(1)
 求证:AA1⊥BC1;
求证:AA1⊥BC1;(2) 求三棱锥A1-ABC的体积.
(1) 略
(2)

(1)证明 : 因为四边形AA1C1C是菱形,所以有AA1=A1C1=C1C=CA= 1.从而知△AA1B是等边三角形. 设D是AA1的中点、连结BD,C1D,则BD⊥AA1,由
1.从而知△AA1B是等边三角形. 设D是AA1的中点、连结BD,C1D,则BD⊥AA1,由 =
=
知C1到AA1的距离为 ∠AA1C1=60°,所以△AA1C1是等边三角形,
∠AA1C1=60°,所以△AA1C1是等边三角形,
且C1D⊥AA1,所以AA1⊥平面BC1D. 又BC1 平面BC1D,故AA1⊥BC1.
平面BC1D,故AA1⊥BC1.
由(1)知BD⊥AA1,又侧面ABB1A1⊥侧面AA1C1C,所以BD⊥平面AA1C1C,
即B到平面AA1C1C 的距离为BD. 又 =
=


 ,BD=
,BD=
所以 =
= =
=
 ·BD=
·BD= ×
× ×
× =
=
故三棱锥A1-ABC的体积为
 1.从而知△AA1B是等边三角形. 设D是AA1的中点、连结BD,C1D,则BD⊥AA1,由
1.从而知△AA1B是等边三角形. 设D是AA1的中点、连结BD,C1D,则BD⊥AA1,由 =
=
知C1到AA1的距离为
 ∠AA1C1=60°,所以△AA1C1是等边三角形,
∠AA1C1=60°,所以△AA1C1是等边三角形, 且C1D⊥AA1,所以AA1⊥平面BC1D. 又BC1
 平面BC1D,故AA1⊥BC1.
平面BC1D,故AA1⊥BC1. 由(1)知BD⊥AA1,又侧面ABB1A1⊥侧面AA1C1C,所以BD⊥平面AA1C1C,
即B到平面AA1C1C 的距离为BD. 又
 =
=


 ,BD=
,BD=
所以
 =
= =
=
 ·BD=
·BD= ×
× ×
× =
=
故三棱锥A1-ABC的体积为


练习册系列答案
相关题目
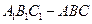 中,
中, 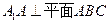 ,
,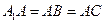 ,
,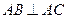 ,点D是
,点D是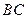 上一点,且
上一点,且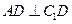 。
。
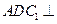 平面
平面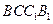 ;
;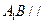 平面
平面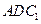 ;
;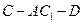 的余弦值
的余弦值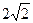 .
.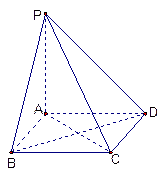
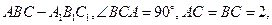
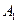 在底面
在底面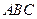 上的射影恰为
上的射影恰为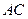 的中点
的中点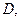 又知
又知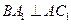 ;
;
 :
: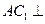 平面
平面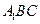 ;
;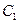 到平面
到平面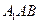 的距离;
的距离;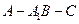 的余弦值;
的余弦值;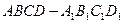 中,
中,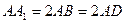 ,且
,且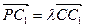
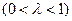 .
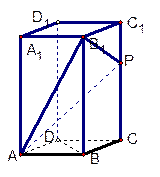
.
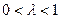 ,总有
,总有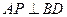 ;
;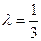 ,求二
,求二 面角
面角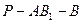 的余弦值;
的余弦值;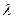 ,使得
,使得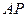 在平面
在平面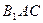 上的射影平分
上的射影平分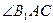 ?若存在,求出
?若存在,求出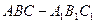 中,
中,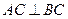 ,
,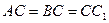 ,
, 是
是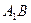 的中点.
的中点.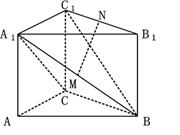
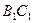 上是否存在一点
上是否存在一点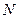 ,使得
,使得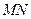 ⊥平面
⊥平面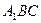 ?若存在,找出点
?若存在,找出点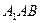 和平面
和平面 ,则异面直线AD与BC所成的角为_______
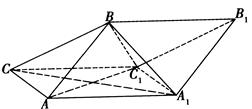
,则异面直线AD与BC所成的角为_______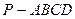 的三视图,E是侧棱PC上的动点.
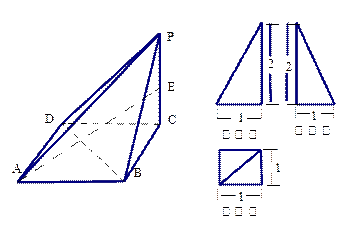
的三视图,E是侧棱PC上的动点.