题目内容
设函数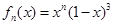 在
在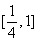 上的最大值为
上的最大值为 (
(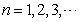 ).
).
(1)求数列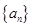 的通项公式;
的通项公式;
(2)求证:对任何正整数n (n≥2),都有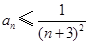 成立;
成立;
(3)设数列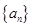 的前n项和为Sn,求证:对任意正整数n,都有
的前n项和为Sn,求证:对任意正整数n,都有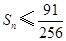 成立.
成立.
(1)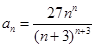 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
解析试题分析:(1)先求得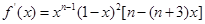 ,令
,令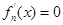 ,得
,得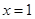 或
或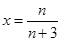 ,因为要考虑根与定义域
,因为要考虑根与定义域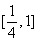 的位置关系,故需讨论n的取值.当
的位置关系,故需讨论n的取值.当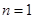 时,
时,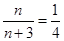 ,此时
,此时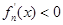 ,函数单调递减;当
,函数单调递减;当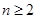 时,
时,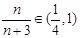 ,将定义域分段,并考虑导函数符号,划分单调区间,判断函数大致图象,进而求最大值,从而求得
,将定义域分段,并考虑导函数符号,划分单调区间,判断函数大致图象,进而求最大值,从而求得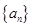 ;(2)由(1)得
;(2)由(1)得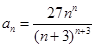 ,将所求证不等式等价变形为,
,将所求证不等式等价变形为,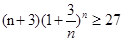 ,再利用二项式定理证明;(3)由(2)得,
,再利用二项式定理证明;(3)由(2)得,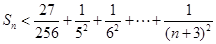 ,再将不等式放缩为可求和的数列问题处理.
,再将不等式放缩为可求和的数列问题处理.
(1)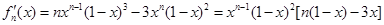
 ,
,
当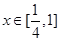 时,由
时,由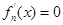 知
知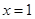 或
或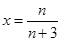 ,
,
当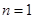 时,则
时,则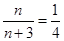 ,
,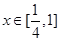 时,
时,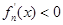 ,
,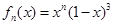 在
在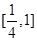 上单调递减,
上单调递减,
所以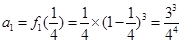
当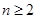 时,
时,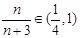 ,
,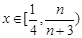 时,
时,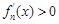 ,
,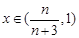 时,
时,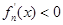 ,
,
∴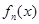 在
在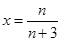 处取得最大值,即
处取得最大值,即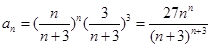 ,
,
综上所述,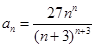 .
.
(2)当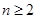 时,要证
时,要证 ,只需证明
,只需证明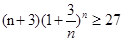
∵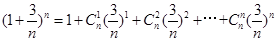
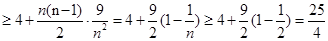
∴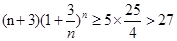 ,所以,当
,所以,当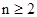 时,都有
时,都有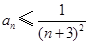 成立.
成立.
(3)当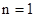 时,结论显然成立;
时,结论显然成立;
当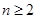 时,由(II)知
时,由(II)知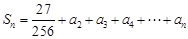
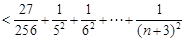
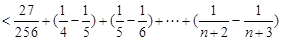
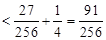 .
.
所以,对任意正整数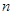 ,都有
,都有 成立. 13分
成立. 13分
考点:1、利用导数求函数的最值;2、二项式定理;3、放缩法.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 平行直线
平行直线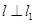 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程. ,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.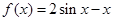 ,
,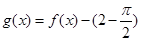 .
.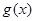 在
在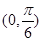 内和在
内和在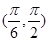 内的零点情况.
内的零点情况.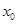 是
是 在
在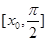 上的最值.
上的最值.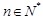 恒有
恒有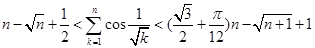 .[来
.[来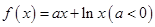 .
.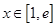 时,函数
时,函数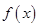 的最大值为
的最大值为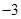 ,求
,求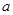 的值;
的值;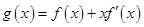 (
(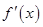 为函数
为函数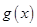 在
在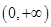 上是单调函数,求
上是单调函数,求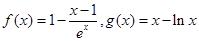 .
.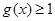 ;
;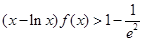 .
.
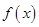 的最大值;
的最大值;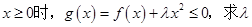 的取值范围.
的取值范围.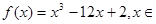 R,求函数
R,求函数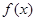 在区间
在区间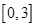 上的最小值.
上的最小值.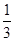 ax3+(a-2)x+c的图象如图所示.
ax3+(a-2)x+c的图象如图所示.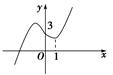
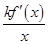 -2ln x在其定义域内为增函数,求实数k的取值范围.
-2ln x在其定义域内为增函数,求实数k的取值范围.