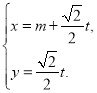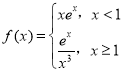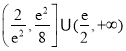题目内容
【题目】设![]() ,已知函数
,已知函数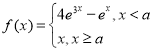 ,
,![]() ,
,![]() ,记函数
,记函数![]() 和
和![]() 的零点个数分别是
的零点个数分别是![]() ,
,![]() ,则( )
,则( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
【答案】A
【解析】
根据题意需分![]() 、
、![]() 和
和![]() 三种情况讨论,为简单起见.只讨论
三种情况讨论,为简单起见.只讨论![]() 的情况,
的情况,![]() 时,分
时,分![]() 和
和![]() 两种情况;
两种情况;![]() 时,根据
时,根据![]() 的取值分五种情况讨论,最后判断即可.
的取值分五种情况讨论,最后判断即可.
解:令![]() ,
,![]() ,
,
![]() ,
,![]() 递增,
递增,
![]() ,
,![]() 递减,
递减,
![]() 时,
时,![]() 有最小值
有最小值![]() ,
,![]()
![]() ,
,
在同一坐标系下,作出函数![]() 和
和![]() 的图象如下,
的图象如下,
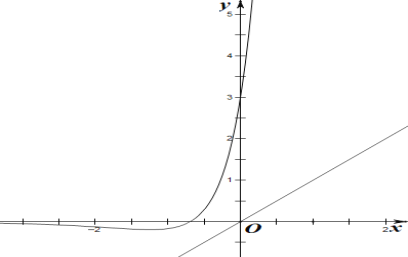
以下分三种情况讨论,
(1)![]() ,作出函数
,作出函数![]() 的图象如下,
的图象如下,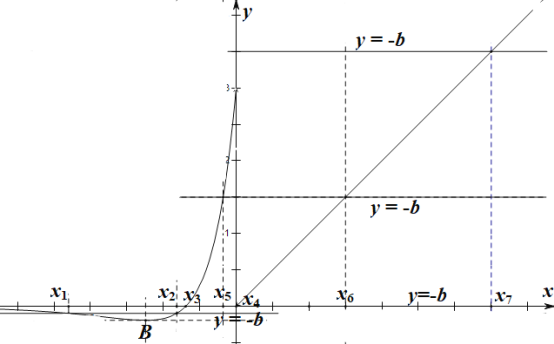
令![]() ,则
,则![]() ,转化为
,转化为![]() 和
和![]() ,
,
若![]() ,函数
,函数![]() 的图象和
的图象和![]() 有2个交点,
有2个交点,
①当![]() 时,
时,![]() 有2个零点,分别记为
有2个零点,分别记为![]() ,且
,且 ![]() ,
,
当![]() 时,即
时,即![]() 显然无解,
显然无解,
当![]() 时,即
时,即![]() 显然无解,所以
显然无解,所以![]() ;
;
②当![]() 时,
时,![]() 有2个零点,分别记为
有2个零点,分别记为![]() ,
,
当![]() 时,即
时,即![]() 显然无解,
显然无解,
当![]() 时,即
时,即![]() 显然有2解,所以
显然有2解,所以![]() ;
;
③当![]() 时,
时,![]() 有2个零点,分别记为
有2个零点,分别记为![]() ,且
,且 ![]() ,
,
当![]() 时,即
时,即![]() 可能有0解、1解、2解,
可能有0解、1解、2解,
当![]() 时,即
时,即![]() 有2解,
有2解,
所以若![]() ,则
,则![]() ,或
,或![]() ,或
,或![]() ,或
,或![]() .
.
若![]() ,即函数
,即函数![]() 的图象和
的图象和![]() 有1个交点,
有1个交点,
④![]() 或
或![]() 时,
时,![]() 有1个零点,此时,
有1个零点,此时,![]() ;
;
⑤![]() 时,
时,![]() 无零点.
无零点.
综合以上有,若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() ,或
,或![]() ,或
,或![]() ,或
,或![]() .
.
(2)![]() 和(3)
和(3)![]() 的情况和(1)相同.
的情况和(1)相同.
所以若![]() ,则
,则![]() ,正确.
,正确.
故选:A.

练习册系列答案
相关题目