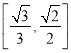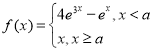题目内容
【题目】已知函数
只能同时满足下列三个条件中的两个：①函数
的最大值为2；②函数的图象可由
的图象平移得到；③函数图象的相邻两条对称轴之间的距离为
.
（1）请写出这两个条件序号，并求出的解析式；
（2）求方程
在区间
上所有解的和.
【答案】（1）满足的条件为①③；
（2）
【解析】
（1）根据题意，条件①②互相矛盾，所以③为函数
满足的条件之一，根据条件③，可以确定函数的最小正周期，进而求得
的值，并对条件①②作出判断，最后求得函数解析式；
（2）将
代入方程
，求得
，从而确定出
或
，结合题中所给的范围，得到结果.
（1）函数满足的条件为①③；
理由如下：由题意可知条件①②互相矛盾，
故③为函数满足的条件之一，
由③可知，
，所以
，故②不合题意，
所以函数满足的条件为①③；
由①可知
，所以；
（2）因为，所以，
所以或，
所以
或
，
又因为
，所以x的取值为
，
，
，
，
所以方程在区间
上所有的解的和为.
练习册系列答案
相关题目
【题目】已知椭圆
的焦点在
轴上，中心在坐标原点，抛物线
的焦点在
轴上，顶点在坐标原点，在、上各取两个点，将其坐标记录于表格中：
|
|
|
|
|
|
|
|
|
|
（1）求、的标准方程；
（2）已知定点
，
为抛物线上的一动点，过点
作抛物线的切线交椭圆于
、
两点，求
面积的最大值．
