题目内容
已知
=(k,1),
=(2,4),若k为满足丨
丨≤4的一随机整数,则△ABC是直角三角形的概率为( )
| AB |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:本题考查的知识点是古典概型,关键是要找出满足△ABC是直角三角形时k的个数,及k的取值范围整数的个数,再根据古典概型的计算公式进行求解.
解答:
解:∵丨
丨=
≤4,
又∵k为整数,则k∈{-3,-2,-1,0,1,2,3}
若△ABC为直角三角形,则
•
=2k+4=0,
当A为直角时,k=-2
当B为直角时,|
|2=|
|2+|
|2,即k=-1或k=3
∵|
|≤4<|
|,∴C不可能为直角.
故△ABC是直角三角形的概率P=
.
| AB |
| k2+1 |
又∵k为整数,则k∈{-3,-2,-1,0,1,2,3}
若△ABC为直角三角形,则
| AB |
| AC |
当A为直角时,k=-2
当B为直角时,|
| AC |
| AB |
| BC |
∵|
| AB |
| AC |
故△ABC是直角三角形的概率P=
| 3 |
| 7 |
点评:本题考查了古典概型求概率,弄清一次试验的意义以及每个基本事件的含义是解决问题的前提,正确把握各个事件的相互关系是解决问题的关键.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
曲线y=x3-3x2+1在点(1,-1)处的切线方程为( )
| A、3x-y-4=0 |
| B、3x+y-2=0 |
| C、4x+y-3=0 |
| D、4x-y-5=0 |
 如图,边长为2的正方形内有一个椭圆,用随机模拟的方法估计该椭圆的面积,在正方形中随机撒了10000粒豆子,落在椭圆内的有8000粒,据此估计该椭圆的面积为( )
如图,边长为2的正方形内有一个椭圆,用随机模拟的方法估计该椭圆的面积,在正方形中随机撒了10000粒豆子,落在椭圆内的有8000粒,据此估计该椭圆的面积为( )| A、3.14 | B、3.2 |
| C、12.56 | D、12.8 |
如图所示程序框图输出的S值是( )


| A、2013 | ||
B、-
| ||
C、
| ||
| D、3 |
在如图的程序图中,输出结果是( )


| A、5 | B、10 | C、20 | D、15 |
已知F是抛物线y2=2x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )
A、
| ||
| B、1 | ||
C、
| ||
D、
|
若A,B是一次试验的两个事件,则“事件A,B对立”是“事件A,B互斥”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
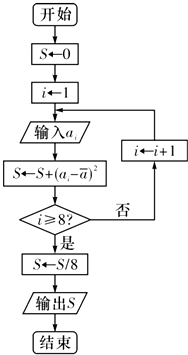 对一个作直线运动的质点的运动过程观测了8次,得到如表所示的数据.
对一个作直线运动的质点的运动过程观测了8次,得到如表所示的数据.