��Ŀ����
7��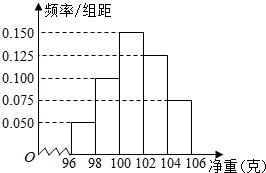 ��������������⣺
��������������⣺��ij�༶һ����52��ѧ�����ֽ��ð�ѧ�������ţ���ϵͳ�����ķ�����ȡһ������Ϊ4����������֪7�ţ�33�ţ�46��ͬѧ�������У���ô������һλͬѧ�ı��Ϊ23��
��һ������1��2��3��3��4��5��ƽ��������������λ����ͬ��
��һ������a��0��1��2��3�����������ݵ�ƽ��ֵΪ1������������Ϊ2��
�ܸ��ݾ���������ع�ϵ������������ͳ���������õĻع�ֱ�߷���Ϊ$\widehat{y}$=bx+a��a=2��$\overline{x}$=1��$\overline{y}$=3����b=1��
����ͼ�Ǹ��ݳ�������ó��IJ�Ʒ�������أ���λ���ˣ����ݻ��Ƶ�Ƶ�ʷֲ�ֱ��ͼ����֪�����в�Ʒ����С��100�˵ĸ�����36���������о��ش��ڻ����98�ˣ�����С��104�˵IJ�Ʒ�ĸ�����90��
������������������
| A�� | �٢ڢ� | B�� | �ڢܢ� | C�� | �ڢۢ� | D�� | �ۢܢ� |
���� �ڢ��У���ϵͳ������ԭ��֪������һλͬѧ�ı��Ϊ20���ڢ��У�������ݵ�ƽ��������λ�����������ж϶Դ����ڢ��У����������ƽ��ֵ�������ķ��������ж϶Դ����ڢ��У��ѣ�1��3������ع�ֱ�߷��̣����ж϶Դ���������������Ϊn����$\frac{36}{n}$=0.300����n=120���ɴ�����������
��� �⣺�ڢ��У���ϵͳ������ԭ��֪�����ļ��Ϊ52��4=13��
�ʳ�ȡ�������ı�ŷֱ�Ϊ7��7+13��7+13��2��7+13��3��
��7�š�20�š�33�š�46�ţ��ʢ��Ǽ����⣻
�ڢ��У�����1��2��3��3��4��5��ƽ����Ϊ$\frac{1}{6}$��1+2+3+4+5��=3��
��λ��Ϊ3������Ϊ3������ͬ���ʢ��������⣻
�ڢ��У������֪������ƽ��ֵΪ1������a+0+1+2+3=5�����a=-1��
�������ķ���Ϊ$\frac{1}{5}[��-1-1��^{2}+��0-1��^{2}+��1-1��^{2}+��2-1��^{2}+��3-1��^{2}]=2$������Ϊ$\sqrt{2}$���ʢ��Ǽ����⣻
�ڢ��У��ع�ֱ�߷���Ϊ$\widehat{y}$=bx+2��ֱ�߹��㣨$\overline{x}��\overline{y}$����
�ѣ�1��3������ع�ֱ�߷���$\widehat{y}$=bx+2����b=1���ʢ��������⣻
�ݲ�Ʒ����С��100�˵�Ƶ��Ϊ��0.050+0.100����2=0.300��
����������Ϊn����$\frac{36}{n}$=0.300����n=120��
���ش��ڻ����98�˲���С��104�˵IJ�Ʒ��Ƶ��Ϊ��0.100+0.150+0.125����2=0.75��
�������о��ش��ڻ����98�˲���С��104�˵IJ�Ʒ�ĸ�����120��0.75=90���ʢ��������⣮
����������������Ϊ���ڢܢݣ�
��ѡ��B��
���� ���������������жϣ��ǻ����⣬����ʱҪ�������⣬ע��ϵͳ������Ƶ�ʷֲ�ֱ��ͼ����������λ����ƽ���������Իع鷽�̵�֪ʶ��ĺ������ã�

| A�� | 2 | B�� | 2$\sqrt{3}$ | C�� | 2$\sqrt{3}$+2 | D�� | 2$\sqrt{3}$-2 |