题目内容
17．α是方程x+lgx=3的根，β是方程x+10x=3的根，则α+β=3．分析 根据题意，构造两函数f（x）=lgx，f-1（x）=10x，由反函数图象间的对称关系得出α+β=3．
解答 解：第一个方程可化为：lgx=3-x，
第二个方程可化为：10x=3-x，
记f（x）=lgx，则其反函数f-1（x）=10x，
它们的图象关于直线y=x轴对称，
根据题意，α，β为f（x），f-1（x）的图象与直线y=3-x交点A，B的横坐标，
由于两交A，B点关于直线y=x对称，
所以，B点的横坐标β就是A点的纵坐标，即A（α，β），
将A（α，β）代入直线y=3-x得，α+β=3，
故答案为：3．
点评 本题主要考查了互为反函数图象间对称性的应用，涉及指数函数与对数函数图象的对称性，以及坐标之间的关系，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
给出下列五个命题：
8．与直线3x-2y=0的斜率相等，且过点（-4，3）的直线方程为（ ）
| A． | y-3=-$\frac{3}{2}$（x+4） | B． | y+3=$\frac{3}{2}$（x-4） | C． | y-3=$\frac{3}{2}$（x+4） | D． | y+3=-$\frac{3}{2}$（x-4） |
12．
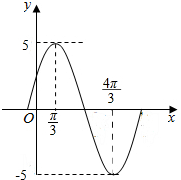函数f（x）=$\sqrt{{a}^{2}+{b}^{2}}$sin（ωx+φ），x∈R，其中a，b，ω都为正数，在一个周期内的图象如图，满足f（x）＜$\frac{{a}^{2}+{b}^{2}}{10}$的x的取值范围是（ ）
函数f（x）=$\sqrt{{a}^{2}+{b}^{2}}$sin（ωx+φ），x∈R，其中a，b，ω都为正数，在一个周期内的图象如图，满足f（x）＜$\frac{{a}^{2}+{b}^{2}}{10}$的x的取值范围是（ ）| A． | （-∞，2kπ），k∈Z | B． | （2kπ-π，2kπ），k∈Z | C． | （2kπ-2π，2kπ），k∈Z | D． | （2kπ-$\frac{4π}{3}$，2kπ），k∈Z |
6．任取k∈[-1，1]，直线L：y=kx+3与圆C：（x-2）2+（y-3）2=4相交于M、N两点，则|MN|≥2$\sqrt{3}$的概率为 （ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{2}$ |