题目内容
若正数x,y满足
+
=5,则3x+4y的最小值是( )
| 3 |
| x |
| 1 |
| y |
A、
| ||
B、
| ||
| C、5 | ||
| D、6 |
考点:基本不等式
专题:不等式的解法及应用
分析:将条件
+
=5进行转化,利用基本不等式的解法即可得到式子的最小值.
| 3 |
| x |
| 1 |
| y |
解答:
解:由于正数x,y满足
+
=5,
则3x+4y=(3x+4y)(
+
)=
+
+
+
≥
+2
=
+2×
=5,
当且仅当
=
,即y=2x,即
+
=
+
=5,
∴x=
,y=
时取等号.
故3x+4y的最小值是5,
故选:C
| 3 |
| x |
| 1 |
| y |
则3x+4y=(3x+4y)(
| 3 |
| 5x |
| 1 |
| 5y |
| 9 |
| 5 |
| 4 |
| 5 |
| 12y |
| 5x |
| 3x |
| 5y |
| 13 |
| 5 |
|
| 13 |
| 5 |
| 6 |
| 5 |
当且仅当
| 12y |
| 5x |
| 3x |
| 5y |
| 3 |
| x |
| 1 |
| y |
| 3 |
| x |
| 1 |
| 2x |
∴x=
| 7 |
| 10 |
| 14 |
| 10 |
故3x+4y的最小值是5,
故选:C
点评:本题主要考查基本不等式的应用,将条件进行转化,利用1的代换是解决本题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
已知函数f(x)=3x2+1,在x=1,△x=0.1时,△y的值为( )
| A、0.63 | B、0.21 |
| C、3.3 | D、0.3 |
设集合A={1,2,3},B={3,4,5},则A∪B=( )
| A、{3} |
| B、{1,2,3,4,5} |
| C、{1,2,3,3,4,5} |
| D、{1,2} |
若p或q为真,¬p为真,则( )
| A、p真q假 | B、p假q真 |
| C、p真q真 | D、p假q假 |
若向量
,
,
的起点M与终点A、B、C互不重合且无三点共线,点O是空间中任一点,则下列选项中的关系肯定能使向量
,
,
构成一个空间基底的是( )
| MA |
| MB |
| MC |
| MA |
| MB |
| MC |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
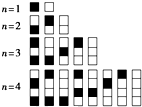 给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示:由此推断,当n=8时,黑色正方形互不相邻的着色方案共有
给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示:由此推断,当n=8时,黑色正方形互不相邻的着色方案共有