题目内容
15.已知函数f(x)=sinx(sinx+$\sqrt{3}$cosx).(1)求f(x)的最小正周期和最大值;
(2)在锐角三角形ABC中,角A,B,C的对边分别为a,b,c,若f($\frac{A}{2}$)=1,a=2$\sqrt{3}$,求三角形ABC面积的最大值.
分析 (1)利用二倍角公式化简f(x);
(2)求出A,根据余弦定理和基本不等式得出bc的最大值,代入面积公式即可.
解答 解:(1)f(x)=sin2x+$\sqrt{3}$sinxcosx=$\frac{1}{2}$-$\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x=sin(2x-$\frac{π}{6}$)$+\frac{1}{2}$.
∴f(x)的最小正周期T=$\frac{2π}{2}$=π,f(x)的最大值是$\frac{3}{2}$.
(2)∵f($\frac{A}{2}$)=sin(A-$\frac{π}{6}$)+$\frac{1}{2}$=1,∴sin(A-$\frac{π}{6}$)=$\frac{1}{2}$,∴A=$\frac{π}{3}$.
∵a2=b2+c2-2bccosA,∴12=b2+c2-bc,∴b2+c2=12+bc≥2bc,∴bc≤12.
∴S=$\frac{1}{2}bcsinA$=$\frac{\sqrt{3}}{4}$bc≤3$\sqrt{3}$.
∴三角形ABC面积的最大值是3$\sqrt{3}$.
点评 本题考查了三角函数的恒等变换,三角函数的性质,解三角形,属于中档题.

练习册系列答案
相关题目
3.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点为F1,F2,P为椭圆上一点,且$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的最小值是2c2,其中$c=\sqrt{{a^2}-{b^2}}$.则椭圆的离心率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
10.阅读如图所示的程序框图,若输入a=$\frac{9}{19}$,则输出的k值是( )
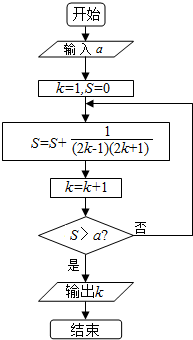

| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
7.底面半径为1,母线长为2的圆锥的体积为( )
| A. | 2π | B. | $\sqrt{3}π$ | C. | $\frac{2π}{3}$ | D. | $\frac{{\sqrt{3}π}}{3}$ |