题目内容
16.已知二阶矩阵A=$[{\begin{array}{l}3&5\\ 0&{-2}\end{array}}]$.(1)求矩阵A的特征值和特征向量;
(2)设向量$\overrightarrow{β}$=$[\begin{array}{l}{1}\\{-1}\end{array}]$,求A2016$\overrightarrow{β}$.
分析 (1)由矩阵A的特征多项式f(λ),令f(λ)=0,求得特征值,代入二元一次方程组求得其特征向量;
(2)由(1)的结论,向量$\overrightarrow{β}$是属于特征值为-2的一个特征向量,利用特征向量的定义与性质即可求得A2016$\overrightarrow{β}$.
解答 解:(1)矩阵A的特征多项式f(λ)=λE-A=$[\begin{array}{l}{λ-3}&{-5}\\{0}&{λ+2}\end{array}]$=(λ-3)(λ+2),
令f(λ)=0,解得:λ1=3,λ2=-2,
将λ1=3,代入二元一次方程组得:$\left\{\begin{array}{l}{0×x-5y=0}\\{0×x+5y=0}\end{array}\right.$,解得y=0,
矩阵A属于特征值3的特征向量为$[\begin{array}{l}{1}\\{0}\end{array}]$,
将λ2=-2,代入二元一次方程组得:$\left\{\begin{array}{l}{-5x-5y=0}\\{0•x+0•y=0}\end{array}\right.$,
当x=1时,y=-1,
∴矩阵A属于特征值-2的特征向量为$[\begin{array}{l}{1}\\{-1}\end{array}]$;
(2)A2016$\overrightarrow{β}$=${λ}_{2}^{2016}$$[\begin{array}{l}{1}\\{-1}\end{array}]$=$[\begin{array}{l}{{2}^{2016}}\\{-{2}^{2016}}\end{array}]$.
∴A2016$\overrightarrow{β}$=$[\begin{array}{l}{{2}^{2016}}\\{-{2}^{2016}}\end{array}]$.
点评 本题考查求二阶矩阵的特征值和特征向量,着重考查特征向量的定义,求法及其性质,属于中档题.

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案| A. | [-$\frac{1}{2}$,+∞) | B. | [-$\frac{3}{2}$,+∞) | C. | [-1,+∞) | D. | [-2,+∞) |
| A. | 2b-$\frac{4}{3}$ | B. | $\frac{3}{2}$b-$\frac{2}{3}$ | C. | 0 | D. | b2-$\frac{1}{6}$b3 |
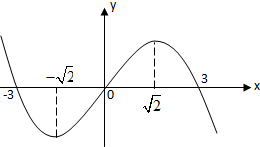
| A. | f(x)极大值为f($\sqrt{2}$),极小值为f(-$\sqrt{2}$) | B. | f(x)极大值为f(-$\sqrt{2}$),极小值为f($\sqrt{2}$) | ||
| C. | f(x)极大值为f(3),极小值为f(-3) | D. | f(x)极大值为f(-3),极小值为f(3) |
| A. | a<$\frac{1}{e}$ | B. | a>$\frac{1}{e}$ | C. | a>$\frac{1}{2}$ | D. | a<$\frac{1}{2}$ |