题目内容
4.解不等式log${\;}_{({x}^{2}+2)}$(3x2-2x-4)>log${\;}_{{x}^{2}+2}$(x2-3x+2)分析 根据x2+2>1,把不等式化为$\left\{\begin{array}{l}{{3x}^{2}-2x-4{>x}^{2}-3x+2}\\{{x}^{2}-3x+2>0}\end{array}\right.$,求出解集即可.
解答 解:不等式log${\;}_{({x}^{2}+2)}$(3x2-2x-4)>log${\;}_{{x}^{2}+2}$(x2-3x+2)中,
∵x2+2>1,
∴原不等式可化为$\left\{\begin{array}{l}{{3x}^{2}-2x-4{>x}^{2}-3x+2}\\{{x}^{2}-3x+2>0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x<-2或x>\frac{3}{2}}\\{x<1或x>2}\end{array}\right.$,
即x<-2或x>2;
∴不等式的解集为(-∞,-2)∪(2,+∞).
点评 本题考查了对数不等式的解法与应用问题,解题的关键是根据对数的单调性转换为普通不等式组,是基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
15.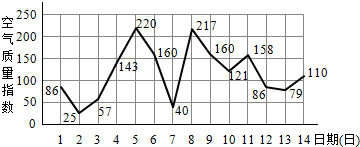 如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表,某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表,某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
(Ⅰ)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(Ⅱ)求此人到达当日空气质量优良的概率;
(Ⅲ)求此人出差期间(两天)空气质量至少有一天为中度或重度污染的概率.
 如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表,某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表,某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).(Ⅰ)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(Ⅱ)求此人到达当日空气质量优良的概率;
(Ⅲ)求此人出差期间(两天)空气质量至少有一天为中度或重度污染的概率.
| 空气质量指数 | 污染程度 |
| 小于100 | 优良 |
| 大于100且小于150 | 轻度 |
| 大于150且小于200 | 中度 |
| 大于200且小于300 | 重度 |
| 大于300且小于500 | 严重 |
| 大于500 | 爆表 |
9.已知1<a≤3,-2<b≤5,则2b-a的取值范围是( )
| A. | (-7,9) | B. | (-4,7) | C. | [-7,9] | D. | [-4,7] |
4.设x∈R,向量$\overrightarrow a=(x,1),\overrightarrow b=(1,-2)$,且$\overrightarrow a⊥\overrightarrow b$,则$|\overrightarrow a|$=( )
| A. | $\sqrt{10}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | 5 |