题目内容
20．函数$f（x）=\sqrt{2x-4}$的单调递增区间是[2，+∞）．分析 可求导数，根据导数符号即可判断f（x）在定义域上为增函数，从而便可得出f（x）的单调递增区间．
解答 解：$f′（x）=\frac{1}{\sqrt{2x-4}}＞0$；
∴f（x）在定义域[2，+∞）上单调递增；
即f（x）的单调递增区间是[2，+∞）．
故答案为：[2，+∞）．
点评 考查根据导数符号判断函数单调性以及求函数单调区间的方法，清楚增函数的定义，注意正确求导．
练习册系列答案
阅读快车系列答案
相关题目
11．某几何体的三视图如图所示，该几何体的体积是（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | 2 | D． | 4 |
8．一个空间几何体的三视图如图所示，则几何体的体积为（ ）
| A． | 2 | B． | $\frac{8}{3}$ | C． | 3 | D． | $\frac{10}{3}$ |
15．已知集合A={0，1，2}，集合B={0，2，4}，则A∩B=（ ）
| A． | {0，1，2} | B． | {0，2} | C． | {0，4} | D． | {0，2，4} |
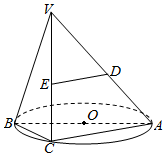如图，AB是⊙O的直径，点C是⊙O上的动点，过动点C的直线VC垂直于⊙O所在的平面，D、E分别是VA、VC的中点．