题目内容
10.已知平面区城D由不等式组$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤4}\\{x-y≤0}\end{array}\right.$确定,M(x,y)为平面区域D内的任意一点,另有一定点A(4,-2),则$\overrightarrow{OM}$$•\overrightarrow{AM}$的最小值为-$\frac{1}{2}$.分析 令z=$\overrightarrow{OM}$$•\overrightarrow{AM}$=(x,y)•(x-4,y+2)=(x-2)2+(y+1)2-5,从而化简可得z+5=(x-2)2+(y+1)2,作平面区域,从而利用数形结合求解即可.
解答 解:令z=$\overrightarrow{OM}$$•\overrightarrow{AM}$=(x,y)•(x-4,y+2)=(x-2)2+(y+1)2-5,
故z+5=(x-2)2+(y+1)2,
由题意作平面区域如下,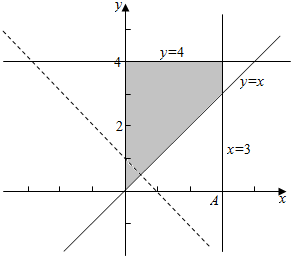 ,
,
(x-2)2+(y+1)2表示了点A(2,-1)与阴影内的点的距离的平方,
故dmin=$\frac{|2+1|}{\sqrt{2}}$,故d2=$\frac{9}{2}$,
故$\overrightarrow{OM}$$•\overrightarrow{AM}$的最小值为$\frac{9}{2}$-5=-$\frac{1}{2}$,
故答案为:-$\frac{1}{2}$.
点评 本题考查了平面向量的数量积及线性规划的变形应用,同时考查了数形结合的思想应用.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
18.设函数f(x)=|2x-1|,c<b<a,且f(c)>f(a)>f(b),则2a+2c与2的大小关系是( )
| A. | 2a+2c>2 | B. | 2a+2c≥2 | C. | 2a+2c≤2 | D. | 2a+2c<2 |
2.函数y=f(x)是定义在R上的可导函数,则“y=f(x)是R上的增函数”是“f′(x)>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |