题目内容

2．方程$y=ax-\frac{1}{a}$表示的直线可能是（　　）
A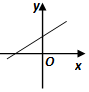．B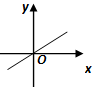．C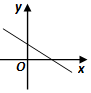．D．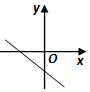

分析 对a分类讨论，利用斜率与截距的意义即可判断出结论．

解答 解：由方程$y=ax-\frac{1}{a}$表示的直线，当a＞0时，斜率k=a＞0，在y轴上的截距=-$\frac{1}{a}$＜0，都不符合此条件．
当a＜0时，斜率k=a＜0，在y轴上的截距=-$\frac{1}{a}$＞0，只有C符合此条件．
故选：C．

点评 本题考查了斜率与截距的意义，考查了分类讨论方法、推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
12．已知函数f（x）=xlnx，g（x）=k（x-1）
（1）当k=e 时，求函数$h（x）=\frac{f（x）-g（x）}{x}$ 的极值；
（2）当k＞0 时，若对任意两个不等的实数x1，x2∈[1，2]，均有$|{\frac{{f（{x_1}）}}{x_1}-\frac{{f（{x_2}）}}{x_2}}|＞|{\frac{{g（{x_1}）}}{x_1}-\frac{{g（{x_2}）}}{x_2}}|$，求实数k 的取值范围；
（3）是否存在实数k，使得函数$h（x）=\frac{f（x）-g（x）}{x}$ 在[1，e]上的最小值为$\frac{1}{2}$，若存在求出k 的值，若不存在，说明理由．
13．在平面直角坐标中，有不共线的三点A，B，C，已知AB，AC所在直线的斜率分别为k1，k2，则“k1k2＞-1”是“∠BAC为锐角”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分也不必要条件
10．已知圆C：（x-a）2+（y-a-2）2=9，其中a为实常数．
（1）若直线l：x+y-4=0被圆C截得的弦长为2，求a的值；
（2）设点A（3，0），O为坐标原点，若圆C上存在点M，使|MA|=2|MO|，求a的取值范围．
17．双曲线$\frac{y^2}{9}-\frac{x^2}{4}=1$的渐近线方程为（　　）
A．$y=±\frac{9}{4}x$B．$y=±\frac{4}{9}x$C．$y=±\frac{2}{3}x$D．$y=±\frac{3}{2}x$
7．已知直线y=-2x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）相交于A，B两点，且线段AB的中点在直线x-4y=0上，则此椭圆的离心率为（　　）
A．$\frac{\sqrt{3}}{3}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{\sqrt{2}}{2}$
14．已知点A，B分别是椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左，右顶点，长轴长为4，离心率为$\frac{1}{2}$．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若点P为椭圆C上除长轴顶点外的任一点，直线AP，PB与直线x=4分别交于点M，N，已知常数λ＞0，求$λ\overrightarrow{PM}•\overrightarrow{PN}+\overrightarrow{PA}•\overrightarrow{PB}$的取值范围．
11．执行如图的程序框图，若输入a=10011，k=2，n=5，则输出的b的值是（　　）
A．38B．39C．18D．19
12．已知命题p：“?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$是奇函数”，则命题?p为（　　）
A．?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$是偶函数B．?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$是奇函数
C．?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$不是奇函数D．?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$不是奇函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网