题目内容
在△ABC中,a2-c2=2b,且4cosAsinC=sinB.
(1)求b;
(2)若S△ABC=2
,求△ABC的周长.
(1)求b;
(2)若S△ABC=2
| 3 |
考点:余弦定理的应用,三角形的面积公式,正弦定理
专题:解三角形
分析:(1)通过正弦定理以及余弦定理化简已知表达式,然后求出的b值.
(2)由已知及正弦定理可求cosA=
=
,得sin2A=1-
,由S△ABC=
bcsinA=2
,可解得c=2,即可求得a,从而可求周长.
(2)由已知及正弦定理可求cosA=
| sinB |
| 4sinC |
| 1 |
| c |
| 1 |
| c2 |
| 1 |
| 2 |
| 3 |
解答:
解:(1)在△ABC中,由sinB=4cosAsinC可得 sin(A+C)=sinAcosC+cosAsinC=4cosAsinC,
化简可得sinAcosC=3cosAsinC,
∴由余弦定理可得:a•
=3c•
,即 2b2=4a2-4c2.
再由a2-c2=2b,可得 2b2=8b,
∴b=4,
(2)∵由(1)可得b=4,
∵4cosAsinC=sinB.
∴由正弦定理可得:cosA=
=
=
,可得sin2A=1-
∵S△ABC=
bcsinA=2
,
∴两边平方可得:12=
b2c2sin2A,化简可得:c2-1=3,可解得:c=2,
∴由a2-c2=2b,可得a=2
∴△ABC的周长=a+b+c=2
+2+4=6+2
.
化简可得sinAcosC=3cosAsinC,
∴由余弦定理可得:a•
| a2+b2-c2 |
| 2ab |
| b2+c2-a2 |
| 2bc |
再由a2-c2=2b,可得 2b2=8b,
∴b=4,
(2)∵由(1)可得b=4,
∵4cosAsinC=sinB.
∴由正弦定理可得:cosA=
| sinB |
| 4sinC |
| b |
| 4c |
| 1 |
| c |
| 1 |
| c2 |
∵S△ABC=
| 1 |
| 2 |
| 3 |
∴两边平方可得:12=
| 1 |
| 4 |
∴由a2-c2=2b,可得a=2
| 2 |
∴△ABC的周长=a+b+c=2
| 2 |
| 2 |
点评:本题主要考查诱导公式、正弦定理以及余弦定理的应用,考查了三角形面积公式的应用,考查计算能力及转化思想,属于中档题.

练习册系列答案
相关题目
若函数f(x)=sin(ωx-
)(ω>0)在区间(0,
)上单调递增,则ω的取值范围是( )
| π |
| 4 |
| π |
| 2 |
A、(0,
| ||
B、[1,
| ||
| C、[1,2] | ||
| D、(0,2] |
已知a=20.2,b=0.80.5,c=log23,则( )
| A、a>b>c |
| B、c>a>b |
| C、a>c>b |
| D、c>b>a |
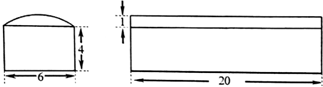
某校新校区建设在市二环路主干道旁,因安全需要,挖掘建设了一条人行地下通道,地下通道设计三视图中的主(正)视力(其中上部分曲线近似为抛物)和侧(左)视图如图(单位:m),则该工程需挖掘的总土方数为( )

| A、560m3 |
| B、540m3 |
| C、520m3 |
| D、500m3 |
设等比数列{an}的前n项和为Sn,且S3=2,S6=6,则a13+a14+a15的值是( )
| A、18 | B、28 | C、32 | D、144 |
复数
的共轭复数为( )
| 1 |
| 1-i |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|