题目内容
设点A,B分别在直线3x-y+5=0和3x-y-13=0上运动,线段AB的中点M恒在直线x+y=4上或者其右上方区域.则直线OM斜率的取值范围是( )
A、(
| ||
| B、[1,3) | ||
| C、(-∞,1]∪(3,+∞) | ||
D、(-∞,1]∪(
|
考点:直线的斜率
专题:直线与圆
分析:设A(x1,y1),B(x2,y2),则3x1-y1-5=0,3x2-y2-13=0,两式相加得3(x1+x2)-(y1+y2)-8=0,设M(x0,y0),则由中点的坐标公式可得3x0-y0-4=0,又点M在直线x+y=4上或者其右上方区域,画图得到M位于以(2,2)为端点向上的射线上,数形结合可得答案.
解答:
解:设A,B两点的坐标为A(x1,y1),B(x2,y2),
∵点A,B分别在直线3x-y+5=0和3x-y-13=0上运动,
∴3x1-y1-5=0,①
3x2-y2-13=0,②
两式相加得3(x1+x2)-(y1+y2)-8=0.
设线段AB的中点M(x0,y0),
则x1+x2=2x0,y1+y2=2y0.
∴3x0-y0-4=0.
即y0=3x0-4.
又M恒在直线x+y=4上或者其右上方区域,
∴线段AB的中点M满足
,如图.
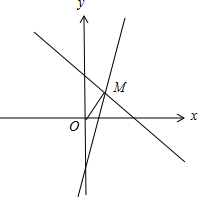
联立
,解得M(2,2),
∴M位于以(2,2)为端点向上的射线上,
当M(2,2)时,kOM=1,
∴直线OM斜率的取值范围是[1,3).
故选:B.
∵点A,B分别在直线3x-y+5=0和3x-y-13=0上运动,
∴3x1-y1-5=0,①
3x2-y2-13=0,②
两式相加得3(x1+x2)-(y1+y2)-8=0.
设线段AB的中点M(x0,y0),
则x1+x2=2x0,y1+y2=2y0.
∴3x0-y0-4=0.
即y0=3x0-4.
又M恒在直线x+y=4上或者其右上方区域,
∴线段AB的中点M满足
|

联立
|
∴M位于以(2,2)为端点向上的射线上,
当M(2,2)时,kOM=1,
∴直线OM斜率的取值范围是[1,3).
故选:B.
点评:本题考查了直线的斜率,考查了数学转化思想方法和数形结合的解题思想方法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将函数y=sin(x+
)(x∈R)的图象上各点的横坐标扩大到原来的2倍(纵坐标不变),再把图象上所有的点向左平行移动
个单位长度,则所得到的图象的解析式为( )
| π |
| 6 |
| π |
| 3 |
A、y=sin(2x+
| ||||
B、y=sin(2x+
| ||||
C、y=sin(
| ||||
D、y=sin(
|
设a=log2m,b=log5m,且
+
=1则m=( )
| 1 |
| a |
| 1 |
| b |
| A、10 | ||
B、
| ||
| C、20 | ||
| D、100 |